PANYA SOCIETY
ฟังก์ชันตรีโกณมิติ
สรุปเนื้อหาที่สำคัญ
เดินทางมาสู่บทที่ 1 ของคณิตศาสตร์ ม.5 เทอม 1 “ฟังก์ชันตรีโกณมิติ” ก็นับว่าเป็นบทสำคัญอย่างยิ่งอีกเช่นกัน เพราะในสถิติข้อสอบ TCAS สัดส่วนการออกข้อสอบบทนี้ ในปีที่ผ่านๆมา ในข้อสอบ A – Level พบความถี่ในการออกข้อสอบสูงสุด โดยเฉลี่ยถึงประมาณ 3-4 ข้อในทุกปี
นับว่าบทเรียนคณิตศาสตร์ ม.5 เทอม 1 เรื่อง “ฟังก์ชันตรีโกณมิติ” มีความสำคัญอย่างยิ่งที่น้อง ๆ จะต้องทำความเข้าใจเนื้อหาโดยละเอียด และอัดพื้นฐานของบทนี้ให้แน่น เพื่อพร้อมรับมือกับการทำข้อสอบที่มีความหลากหลาย และควรฝึกทำโจทย์ที่ประยุกต์หลายบทเข้าไว้ด้วยกัน ที่มีเนื้อหาร่วมกับบทนี้
อย่างที่กล่าวข้างต้น ฟังก์ชันตรีโกณมิติ ออกข้อสอบหลายข้อจริง ๆ ดังนั้น น้อง ๆ ก็ควรใช้เป็นข้อที่ทำคะแนนอย่างยิ่ง เพื่อให้การอ่านหนังสือเตรียมสอบเข้ามหาวิทยาลัยคุ้มค่าที่สุด
ฟังก์ชันตรีโกณมิติ มีหน่วยย่อย ดังนี้
- ทบทวนบทเรียนเรื่องตรีโกณมิติ
- มุมเรเดียนและวงกลมหนึ่งหน่วย
- ฟังก์ชันตรีโกณมิติ
- ทบทวนเครื่องหมายของฟังก์ชันตรีโกณมิติ
- กราฟของฟังก์ชันตรีโกณมิติ
- เอกลักษณ์ตรีโกณมิติ
- สูตรตรีโกณมิติ
- ตัวผกผันของฟังก์ชันตรีโกณมิติ
- สมการตรีโกณมิติ
- กฎของโคไซน์และกฎของไซน์
- การแก้ปัญหาโดยใช้ตรีโกณมิติ
ทบทวนบทเรียนเรื่องตรีโกณมิติ
มุมภายในของรูปสามเหลี่ยม
มุมภายในของรูปสามเหลี่ยม มีผลรวมเท่ากับ 180°
สามเหลี่ยมมุมฉาก
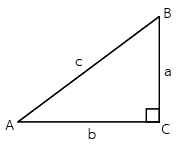
ทฤษฎีบทพีทาโกรัส
a2 + b2 = c2
สามเหลี่ยมคล้าย
สามเหลี่ยมสองรูป จะคล้ายกันเมื่อมีมุมเท่ากันทั้งสามคู่
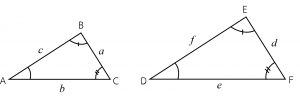
△ AฺBC ~ △ DEF
จะได้ว่า อัตราส่วนของด้านที่อยู่ระหว่างมุมเดียวกัน จะมีอัตราส่วนเท่ากัน
เช่น
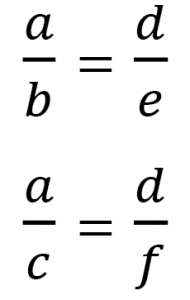
อัตราส่วนตรีโกณมิติ
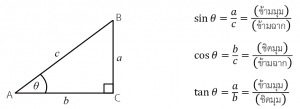
***ข้อควรรู้***
เมื่อเรารู้ความยาวด้านสองด้านของสามเหลี่ยมมุมฉาก จะหาความยาวอีกด้านได้จากทฤษฎีบทพีทาโกรัส ดังนั้น เราจะหาอัตราส่วนตรีโกณมิติทั้งหมดได้เสมอ เมื่อรู้ความยาวด้านเพียงสองด้าน
ค่าตรีโกณมิติของมุมที่พบบ่อย

กราฟของฟังก์ชันตรีโกณมิติ
– กราฟของ y = sin x
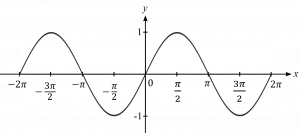
– กราฟของ y = cos x
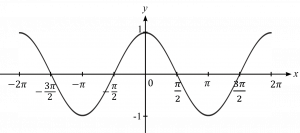
– กราฟของ y = tan x
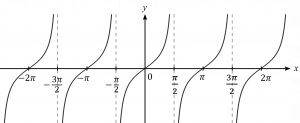
– กราฟของ y = cot x
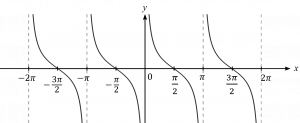
– กราฟของ y = sec x
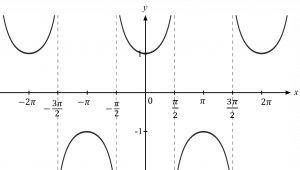
– กราฟของ y = cosec x
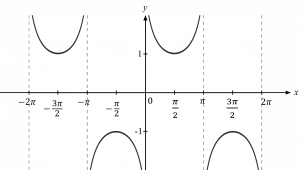
การแปลงกราฟของฟังก์ชันไซน์และโคไซน์
– คาบ คือ ความยาวของช่วงที่สั้นที่สุดที่ทำให้กราฟของฟังก์ชันมีลักษณะเหมือนกันกับช่วงอื่น ๆ
– แอมพลิจูด คือ ครึ่งหนึ่งของผลต่างระหว่างค่าสูงสุดและค่าต่ำสุดของฟังก์ชัน
กำหนดให้ C เป็นค่าคงที่ ซึ่งไม่เท่ากับ 0
• sin(Cx) หรือ cos(Cx) : คาบ = 2π/|C| เรนจ์ = [-1, 1] แอมพลิจูด = 1
• sin x + C หรือ cos x + C : คาบ = 2π เรนจ์ = [C-1, C+1] แอมพลิจูด = 1
• C sin x หรือ C cos x : คาบ = 2π เรนจ์ = [-|C|, |C|] แอมพลิจูด = |C|
เอกลักษณ์ตรีโกณมิติ
กำหนดให้ n เป็นจำนวนเต็ม
sin2 θ + cos2 θ = 1
sec2 θ = tan2 θ + 1
cosec2 θ = cot2 θ + 1
sin (θ + 2nπ) = sin θ
cos (θ + 2nπ) = cos θ
tan (θ + 2nπ) = tan θ
sec (θ + 2nπ) = sec θ
cosec (θ + 2nπ) = cosec θ
cot (θ + 2nπ) = cot θ
sin (-θ ) = – sin θ
cos (-θ ) = cos θ
tan (-θ ) = – tan θ
sec (-θ ) = sec θ
cosec (-θ ) = – cosec θ
cot (-θ ) = – cot θ
สูตรตรีโกณมิติ
สูตรผลบวกและผลต่างของมุม
sin(A+B) = sin A cos B + cos A sin B
sin(A-B) = sin A cos B – cos A sin B
cos(A+B) = cos A cos B – sin A sin B
cos(A-B) = cos A cos B + sin A sin B
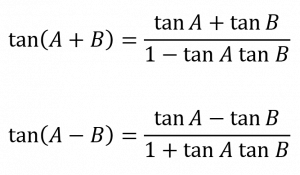
สูตรมุมสองเท่า
sin 2A = 2 sin A cos A
cos 2A = cos2 A – sin2 A
= 1 – 2 sin2 A
= 2 cos2 A – 1 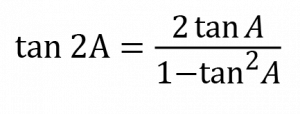
สูตรมุมครึ่งเท่า
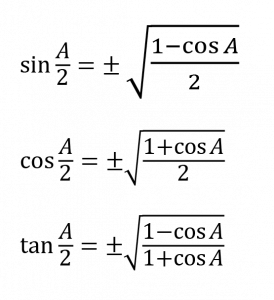
สูตรผลคูณของ sin กับ cos
2 cos A cos B = cos(A+B) + cos(A-B)
-2 sinA sinB = cos(A+B) – cos(A-B)
2 sinA cosB = sin(A+B) + sin(A-B)
2 cosA sinB = sin(A+B) – sin(A-B)
ตัวผกผันของฟังก์ชันตรีโกณมิติ
ตัวผกผันของฟังก์ชันตรีโกณมิติ เขียนแทนด้วย arc ตามด้วยฟังก์ชันตรีโกณมิติ หรือ ฟังก์ชันตรีโกณมิติ-1
เช่น จาก sin θ = 1
จะได้ arcsin(1) = θ = sin-1(1) = 90°
เรนจ์ของฟังก์ชัน arc
arcsin : [-90°, 90°]
arctan : (-90°, 90°)
arccosec : [-90°, 90°] – {0°}
arccos : [0°, 180°]
arccot : (0°, 180°)
arcsec : [0°, 180°] – {90°}
เทคนิคการหาค่าของฟังก์ชันตรีโกณมิติผกผัน
1. ไม่สนใจเครื่องหมายของค่าในฟังก์ชันตรีโกณมิติผกผัน ให้หาค่า θ ของค่าบวกก่อน
2. พิจารณาว่า θ ควรอยู่ในจตุภาคใด โดยดูจากเรนจ์ของฟังก์ชันตรีโกณมิติผกผันนั้น
ตัวอย่างโจทย์
จงหา sec -1(-2) เฉลย
เทคนิคการหาค่าของฟังก์ชันตรีโกณมิติจากมุม arc
1. กำหนดมุม arc เป็นมุม θ
2. วาดรูปสามเหลี่ยมมุมฉากของมุม α ซึ่งมีค่าฟังก์ชันตรีโกณมิติ เท่ากับ |ค่าฟังก์ชันตรีโกณมิติของมุม θ|
3. หาค่าของฟังก์ชันตรีโกณมิติที่ต้องการ จากรูปสามเหลี่ยมมุมฉากของมุม α
4. พิจารณาเครื่องหมายของค่าฟังก์ชันตรีโกณมิติที่ต้องการ โดยการพิจารณาว่ามุม θ อยู่จตุภาคใด
ตัวอย่างโจทย์
จงหา sin(2 arctan (2)) เฉลย
สมการตรีโกณมิติ
เทคนิคการแก้สมการตรีโกณมิติ
1. เปลี่ยน cosec, sec, cot ไปเป็น sin, cos, tan
2. ปรับสมการให้เหลือฟังก์ชันตรีโกณมิติน้อยที่สุด
3. ใช้สูตรหรือเอกลักษณ์ตรีโกณมิติต่าง ๆ ปรับสมการให้อยู่ในรูป ผลคูณ = 0
4. ใช้การแก้สมการตัวแปรเดียวหรือการแก้สมการพหุนาม มาช่วยแก้
เช่น tan2 θ – 3 tan θ + 2 = 0
(tan θ – 2)(tan θ – 1) = 0
5. ตรวจเครื่องหมายของคำตอบและช่วงของคำตอบให้ดี เพื่อให้ได้คำตอบครบ ถูกต้อง และไม่เกิน
ตัวอย่างโจทย์
จงแก้สมการ cos 2θ + 5 sin θ + 2 = 0 เฉลย
กฎของไซน์และกฎของโคไซน์
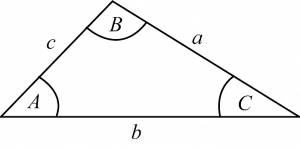
กฎของไซน์
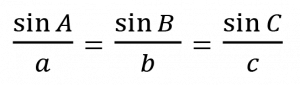
กฎของโคไซน์
a2 = c2 + b2 – 2bc cos A
การแก้ปัญหาโดยใช้ตรีโกณมิติ
1. วาดรูป เพื่อให้เห็นภาพและสามารถวิเคราะห์โจทย์ได้ง่ายขึ้น
2. หาข้อมูลที่เรารู้จากโจทย์
3. ตีความโจทย์ ว่าต้องการให้หาอะไร
4. ใช้ความรู้เกี่ยวกับตรีโกณมิติในการแก้ปัญหา
ตัวอย่างโจทย์
เจนนี่ยืนอยู่บนสนามแห่งหนึ่งมองเห็นยอดเสาธงเป็นมุมเงย 15° แต่เมื่อตรงเข้าไปหาเสาธงอีก 60 เมตร เขามองเห็นยอดเสาธงเป็นมุมเงย 75° ถ้าเจนนี่สูง 165° เซนติเมตร จงหาความสูงของเสาธง
คุยกันท้ายบท
จะเห็นได้ว่า “ฟังก์ชันตรีโกณมิติ” ในคณิตศาสตร์ ม.5 เทอม 1 จะมีความเชื่อมโยงกับบทที่ผ่านมาคือ “ความสัมพันธ์ และฟังก์ชัน” ซึ่งถ้าน้องคนไหน ไม่มีความรู้ความเข้าใจที่แท้จริงจากบทที่แล้ว ก็จะยิ่งสร้างปมปัญหาต่อมาถึงบทนี้ ดังนั้น ควรกลับไปทบทวน “ความสัมพันธ์ และฟังก์ชัน” จะได้นำความรู้ความเข้าใจจากบทที่แล้ว มาต่อยอดได้ในเนื้อหาของบทนี้
ที่สำคัญคือ อย่าลืมฝึกทำโจทย์บ่อย ๆ และใช้เวลาว่างบนหน้าเว็บไซต์ของ Panya Society ลองฝึกทำโจทย์ที่พี่ให้ไว้ หรือเข้าไปชมตัวอย่างวิดีโอการสอนต่าง ๆ พร้อมคิดคำนวณตามไปด้วย เพื่อให้ได้ประโยชน์จากการทบทวนความรู้ครับ แล้วพบกันในบทต่อไป เข้มข้นยิ่งขึ้นกับ “เมทริกซ์” มีรูปแบบการคิดแบบใหม่ สนุกแน่นอนครับผม 🙂
พี่หวังว่า น้อง ๆ จะสนุกกับการเรียนคณิตศาสตร์ ม.5 เทอม 1 ไปตลอดทั้งเทอม ขอให้น้อง ๆ ประสบความสำเร็จในการเรียน ได้เกรดดังหวัง คะแนนปังทุกคนเลยครับ แวะไปชมเนื้อหาบทต่อไปของคณิตศาสตร์ ม.5 เทอม 1 กันด้วยนะ…อย่าเทพี่แชร์และพี่ปิงกลางทางนะครับ
- อดีต Senior Software Engineer ที่ Google กว่า 10 ปี
- ได้รับทุนเล่าเรียนหลวงไปศึกษาระดับปริญญาตรี ด้าน Electrical and Computer Engineering และ Computer Science ที่ Carnegie Mellon University สหรัฐอเมริกา
- จบปริญญาเอก ด้าน Artificial Intelligence พร้อมรางวัลนักเรียนดีเด่นจาก UCLA
- ผลงานวิจัยด้าน Artificial Intelligence (AI) ของพี่นอตได้รับรางวัลงานวิจัยดีเยี่ยมจาก สำนักงานคณะกรรมการวิจัยแห่งชาติในปี 2557
ตัวอย่างการสอน โดยพี่นอต
Math Magic















