PANYA SOCIETY
เมทริกซ์
สรุปเนื้อหาที่สำคัญ
เดินทางมาสู่บทที่ 2 ของคณิตศาสตร์ ม. 5 เทอม 1 “เมทริกซ์” ก็นับว่าเป็นบทสำคัญอย่างยิ่งอีกเช่นกัน เพราะในสถิติข้อสอบ TCAS สัดส่วนการออกข้อสอบบทนี้ ในปีที่ผ่าน ๆ มา ในข้อสอบ A – Level พบความถี่ในการออกข้อสอบโดยเฉลี่ยถึงประมาณ 1 – 2 ข้อในทุกปี
นับว่าบทเรียนคณิตศาสตร์ ม. 5 เทอม 1 เรื่อง “เมทริกซ์” มีความสำคัญอย่างยิ่งที่น้อง ๆ จะต้องทำความเข้าใจเนื้อหาโดยละเอียด และอัดพื้นฐานของบทนี้ให้แน่น เพื่อพร้อมรับมือกับการทำข้อสอบที่มีความหลากหลาย และควรฝึกทำโจทย์ที่ประยุกต์หลายบทเข้าไว้ด้วยกัน ที่มีเนื้อหาร่วมกับบทนี้
อย่างที่กล่าวข้างต้น เมทริกซ์ มีออกข้อสอบทุกปี ดังนั้น น้อง ๆ ก็ควรใช้เป็นข้อที่ทำคะแนนอย่างยิ่ง เพื่อให้การอ่านหนังสือเตรียมสอบเข้ามหาวิทยาลัยคุ้มค่าที่สุด
เมทริกซ์ มีหน่วยย่อย ดังนี้
- ระบบสมการเชิงเส้น
- เมทริกซ์และชนิดของเมทริกซ์
- ทรานสโพสและการเท่ากันของเมทริกซ์
- การบวก การคูณ และการยกกำลังของเมทริกซ์
- ดีเทอร์มิแนนต์ ไมเนอร์ และโคแฟกเตอร์
- ตัวผกผันของเมทริกซ์
- การแก้ระบบสมการโดยใช้เมทริกซ์
ระบบสมการเชิงเส้น
สมการเชิงเส้น คือ สมการที่ตัวแปรทุกตัวมีเลขยกกำลังเป็น 1
สมการเชิงเส้นตัวแปรเดียว สามารถแก้สมการได้ตามปกติ
เช่น 2x + 1 = 5
2x = 4
x = 2
สมการเชิงเส้น 2 ตัวแปร สามารถแก้สมการได้เมื่อมี 2 สมการ
เช่น x + 3y = 8 เป็นสมการที่ (1)
x – 2y = 3 เป็นสมการที่ (2)
คูณแต่ละสมการด้วยค่าคงที่ แล้วนำมาบวกลบกัน เพื่อกำจัด 1 ตัวแปร
นำ (1) – (2) : x + 3y – (x – 2y) = 8 – 3
5y = 5
y = 1
แทน y = 1 ใน (1) : x + 3(1) = 8
x = 5
สมการเชิงเส้น 3 ตัวแปร สามารถแก้สมการได้เมื่อมี 3 สมการ
เช่น ระบบสมการ
x + y + z = 2 เป็นสมการที่ (1)
x + y – z = 4 เป็นสมการที่ (2)
x + 2y + z = 4 เป็นสมการที่ (3)
นำ (1) – (2) : 2z = -2
z = -1
แทน z = -1 ใน (1) : x + y – 1 = 2
x + y = 3 เป็นสมการที่ (4)
แทน z = -1 ใน (2) : x + y + 1 = 4
x + y = 3
แทน z = -1 ใน (3) : x + 2y – 1 = 4
x + 2y = 5 เป็นสมการที่ (5)
นำ 2×(4) – (5) : 2x + 2y – (x + 2y) = 6 – 5
x = 1
แทน x = 1 ใน (4) : 1 + y = 3
y = 2
ดังนั้น x = 1, y = 2, z = -1
เนื่องจากสมการเชิงเส้น 2 ตัวแปร คือ สมการเส้นตรง จึงอาจหาคำตอบของระบบสมการ 2 สมการ ได้ 3 แบบ
1. หาคำตอบได้แน่นอน ในกรณีที่สมการเส้นตรงทั้งสองไม่ขนานกัน
2. หาคำตอบไม่ได้ ในกรณีที่สมการเส้นตรงทั้งสองขนานกัน และไม่ใช่เส้นตรงเดียวกัน
3. มีคำตอบมากมายไม่จำกัด ในกรณีที่สมการเส้นตรงทั้งสองเป็นเส้นตรงเดียวกัน
เมทริกซ์และชนิดของเมทริกซ์
เมทริกซ์ คือ สิ่งที่เก็บข้อมูลกลุ่มหนึ่งไว้ โดยตำแหน่งของข้อมูลมีความสำคัญ ไม่สามารถสลับตำแหน่งของข้อมูลได้ สามารถเขียนได้โดย นำข้อมูลมาเขียนเรียนเป็นแถวและหลัก ไว้ในวงเล็บ [ ]
เช่น

กำหนดเมทริกซ์

- เมทริกซ์ A มีขนาด (มิติ) m × n หมายความว่า เมทริกซ์ A มีจำนวน m แถว และมี n หลัก
- เรียกสมาชิกที่อยู่ตำแหน่ง แถวที่ i หลักที่ j ว่า aij
ชนิดของเมทริกซ์
1. เมทริกซ์แถว คือ เมทริกซ์ที่มีเพียง 1 แถว ซึ่งจะมีมิติ = 1 × n
2. เมทริกซ์หลัก คือ เมทริกซ์ที่มีเพียง 1 หลัก ซึ่งจะมีมิติ = m × 1
3. เมทริกซ์ศูนย์ คือ เมทริกซ์ที่มีสมาชิกทุกตัวเป็น 0
4. เมทริกซ์จตุรัส คือ เมทริกซ์ที่มีจำนวนแถวเท่ากับจำนวนหลัก ซึ่งจะมีมิติ = k × k
5. เมทริกซ์เอกลักษณ์ คือ เมทริกซ์จัตุรัสที่มีสมาชิกในแนวทแยงมุมหลัก (แนวทแยงมุมจากบนซ้ายไปล่างขวา) เป็นเลข 1 และสมาขิกที่เหลือเป็น 0
6. เมทริกซ์ทแยงมุม คือ เมทริกซ์ที่มีสมาชิกซึ่งไม่อยู่ในแนวทแยงมุมหลักเป็น 0 ทั้งหมด
7. เมทริกซ์สเกลาร์ คือ เมทริกซ์จัตุรัสที่มีสมาชิกในแนวทแยงมุมหลักมีค่าเท่ากัน และสมาชิกที่เหลือเป็น 0
8. เมทริกซ์สามเหลี่ยมบน คือ เมทริกซ์จัตุรัสที่มีสมาชิกที่อยู่ใต้แนวทแยงมุมหลักมีค่าเป็น 0
9. เมทริกซ์สามเหลี่ยมล่าง คือ เมทริกซ์จัตุรัสที่มีสมาชิกที่อยู่เหนือแนวทแยงมุมหลักมีค่าเป็น 0
ทรานสโพสและการเท่ากันของเมทริกซ์
ทรานสโพสของเมทริกซ์ คือ เมทริกซ์ที่เกิดจากการสลับให้แถวเป็นหลัก ให้หลักเป็นแถว
ทรานสโพสของเมทริกซ์ A เขียนแทนด้วย At
เช่น
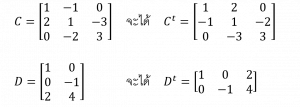
- สมาชิกในแถวที่ i หลักที่ j ของเมทริกซ์ A จะมีค่าเท่ากับ สมาชิกในแถวที่ j หลักที่ i ของเมทริกซ์ At
- ถ้าเมทริกซ์ A มีมิติ = m × n แล้วเมทริกซ์ At มีมิติ = n × m
- เมทริกซ์ (At)t จะเท่ากับ เมทริกซ์ A
- ถ้าเมทริกซ์ At = A จะได้ว่า เมทริกซ์ A เป็น เมทริกซ์สมมาตร
การคูณเมทริกซ์ด้วยค่าคงที่
ให้ k เป็นค่าคงที่
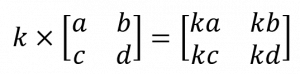
- ถ้าเมทริกซ์ At = -A จะได้ว่า เมทริกซ์ A เป็น เมทริกซ์เสมือนสมมาตร
การเท่ากันของเมทริกซ์
เมทริกซ์จะเท่ากันได้ เมื่อมีมิติเท่ากัน และสมาชิกตำแหน่งเดียวกันมีค่าเท่ากัน
เช่น
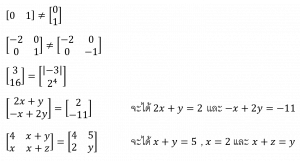
การบวก การคูณ และการยกกำลังของเมทริกซ์
การบวกเมทริกซ์
เมทริกซ์จะบวกหรือลบกันได้เมื่อมีมิติเท่ากัน โดยนำตัวที่อยู่ตำแหน่งเดียวกันมาบวกหรือลบกัน
เช่น

สมบัติของการบวกเมทริกซ์
ให้ A, B, C เป็นเมทริกซ์ c, d เป็นค่าคงที่ และ 0 เป็นเมทริกซ์ศูนย์
1. มิติของ A + B = มิติของ A = มิติของ B
2. A + B = B + A
3. (A + B) + C = A + (B + C)
4. A + 0 = 0 + A = A
5. A + (-A) = (-A) + A = 0
6. c(A + B) = cA + cB
7. (c + d)A = cA + dA
8. (cd)A = c(dA) = (dc)A = d(cA)
9. 1A = A
10. 0A = 0
การคูณเมทริกซ์
1. เมทริกซ์ A จะคูณกับ B ได้ เมื่อจำนวนหลักของ A เท่ากับจำนวนแถวของ B
ถ้า A มีมิติ m × n และ B มีมิติ n × p จะได้ A × B มีมิติ m × p
2. ให้ C = A × B
จะได้ว่า Cxy หาได้จาก การนำแถวที่ x ของ A มากระทำกับหลักที่ y ของ B
โดย Cxy = (ตัวที่ 1 ของแถว A)(ตัวที่ 1 ของหลัก B) + (ตัวที่ 2 ของแถว A)(ตัวที่ 2 ของหลัก B) + …
เช่น
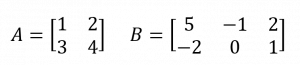
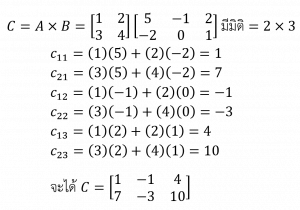
สมบัติของการคูณเมทริกซ์
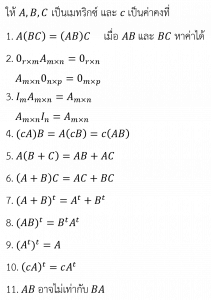
เมทริกซ์ยกกำลัง
เมทริกซ์ที่ยกกำลังได้ จะต้องเป็นเมทริกซ์จตุรัส
เช่น

ดีเทอร์มิแนนต์ ไมเนอร์ และโคแฟกเตอร์
ดีเทอร์มิแนนต์
เป็นคุณสมบัติของเมทริกซ์จัตุรัส มีค่าเป็นจำนวนจริง
ดีเทอร์มิแนนต์ของ A เขียนแทนด้วย det A = |A|
เมทริกซ์ 2 × 2 หา det โดยการคูณแนวทแยงมุมหลัก ลบด้วยการคูณแนวทแยงมุมจากล่างซ้ายไปบนขวา
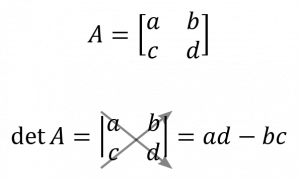
เมทริกซ์ 3 × 3 หา det ได้โดยเติมสองหลักแรกต่อจากเมทริกซ์เดิม
แล้วหา det โดยคูณแนวทแยงมุมจากบนซ้ายไปล่างขวา ลบด้วย คูณแนวทแยงมุมจากล่างซ้ายไปบนขวา
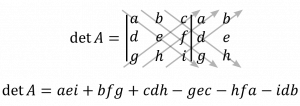
ข้อควรรู้
- เมทริกซ์ที่มี det เท่ากับ 0 เรียกว่า เมทริกซ์เอกฐาน
- เมทริกซ์ที่มี det ไม่เท่ากับ 0 เรียกว่า เมทริกซ์ไม่เอกฐาน
ไมเนอร์

โคแฟกเตอร์

คุณสมบัติของดีเทอร์มิแนนต์
ให้ A, B เป็นเมทริกซ์ I เป็นเมทริกซ์เอกลักษณ์ n เป็นจำนวนเต็มบวก และ c เป็นค่าคงที่
1. ถ้า A มีแถวหรือหลักใดเป็น 0 ทั้งหมด แล้ว det A = 0
2. ถ้า A มีแถวหรือหลักใดซ้ำกัน แล้ว det A = 0
3. ถ้า A เป็นเมทริกซ์สามเหลี่ยมบน หรือสามเหลี่ยมล่าง แล้ว det A = ผลคูณของแนวทแยงมุมหลัก
4. det(AB) = det(A)∙det(B)
5. det(An)= (detA)n
6. det(I) = 1
7. det(At) = det(A)
8. ถ้า B เกิดจากการนำ c ไปคูณแถวหรือหลักหนึ่งของ A แล้ว det B = c det A
9. det(cA) = cn det A เมื่อ A มีมิติ = n × n
10. det(0) = 0
11. ถ้า B เกิดจากการสลับแถวหรือสลับหลักของ A แล้ว det B = -det A
12. ถ้า B เกิดจากการนำ c ไปคูณแถวหรือหลักหนึ่งของ A แล้วนำไปบวกกับแถวหรือหลักอื่นของ A
จะได้ det B = det A
ตัวผกผันของเมทริกซ์
เมทริกซ์ผกผันของ A คือ เมทริกซ์ที่เมื่อนำมาคูณกับ A แล้วได้เป็นเมทริกซ์เอกลักษณ์
เมทริกซ์ผกผันของ A เขียนแทนด้วย A-1
จะได้ว่า A A-1 = A-1 A = In
เมทริกซ์ 2 × 2

สมบัติของเมทริกซ์ผกผัน
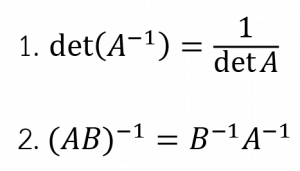
การแก้ระบบสมการโดยใช้เมทริกซ์
การแก้ระบบสมการด้วยเมทริกซ์แต่งเติม
1. เขียนระบบสมการ ในรูปสมการเมทริกซ์ AX = B
2. แต่งเติมเมทริกซ์ A ด้วยเมทริกซ์ B แล้วใช้การดำเนินการตามแถว
ทำให้เมทริกซ์ A กลายเป็นเมทริกซ์ขั้นบันไดแบบแถว โดยจะมีลักษณะดังนี้
1.) ในแต่ละแถว ตัวเลขแรกที่ไม่ใช่ 0 ต้องเป็นเลข 1
2.) ตัวเลขที่อยู่ใต้เลข 1 ตัวแรก ต้องเป็น 0
3.) เลข 0 ที่อยู่ก่อนเลข 1 ตัวแรก จะต้องเพิ่มขึ้นทุกแถว
4.) ถ้ามีแถวที่เป็น 0 ทั้งหมด แถวต่อ ๆ ไป ต้องเป็นศูนย์ทั้งหมด
3. เขียนระบบสมการใหม่ จากเมทริกซ์ขั้นบันไดแบบแถว จะได้ค่าของตัวแปร 1 ตัว
4. แทนค่าตัวแปรที่ได้ในสมการอื่น เพื่อหาค่าตัวแปรที่เหลือ
การแก้ระบบสมการด้วยกฎของเครเมอร์
1. เขียนระบบสมการ ในรูปสมการเมทริกซ์ AX = B
2. หา x1 โดยการหา det ของเมทริกซ์ที่เกิดจากการแทนที่หลักที่ 1 ของ A ด้วย B แล้วหารด้วย det A
3. หา xn โดยการหา det ของเมทริกซ์ที่เกิดจากการแทนที่หลักที่ n ของ A ด้วย B แล้วหารด้วย det A
คุยกันท้ายบท
จะเห็นได้ว่า “เมทริกซ์” ในคณิตศาสตร์ ม.5 เทอม 1 จะมีความเชื่อมโยงกับบทที่ผ่านมาคือ “จำนวนจริง” ซึ่งถ้าน้องคนไหน ไม่มีความรู้ความเข้าใจที่แท้จริงจากบทก่อนหน้านี้ ก็จะยิ่งสร้างปมปัญหาต่อมาถึงบทนี้ ดังนั้น ควรกลับไปทบทวน “จำนวนจริง” จะได้นำความรู้ความเข้าใจจากบทที่แล้ว มาต่อยอดได้ในเนื้อหาของบทนี้
ที่สำคัญคือ อย่าลืมฝึกทำโจทย์บ่อย ๆ และใช้เวลาว่างบนหน้าเว็บไซต์ของ Panya Society ลองฝึกทำโจทย์ที่พี่ให้ไว้ หรือเข้าไปชมตัวอย่างวิดีโอการสอนต่าง ๆ พร้อมคิดคำนวณตามไปด้วย เพื่อให้ได้ประโยชน์จากการทบทวนความรู้ครับ แล้วพบกันในบทต่อไป เข้มข้นยิ่งขึ้นกับ “เวกเตอร์” มีรูปแบบการคิดแบบใหม่ สนุกแน่นอนครับผม 🙂
พี่หวังว่า น้องๆจะสนุกกับการเรียนคณิตศาสตร์ ม. 5 เทอม 1 ไปตลอดทั้งเทอม ขอให้น้อง ๆ ประสบความสำเร็จในการเรียน ได้เกรดดังหวัง คะแนนปังทุกคนเลยครับ แวะไปชมเนื้อหาบทต่อไปของคณิตศาสตร์ ม. 5 เทอม 1 กันด้วยนะ…อย่าเทพี่นอตกลางทางนะครับ
- อดีต Senior Software Engineer ที่ Google กว่า 10 ปี
- ได้รับทุนเล่าเรียนหลวงไปศึกษาระดับปริญญาตรี ด้าน Electrical and Computer Engineering และ Computer Science ที่ Carnegie Mellon University สหรัฐอเมริกา
- จบปริญญาเอก ด้าน Artificial Intelligence พร้อมรางวัลนักเรียนดีเด่นจาก UCLA
- ผลงานวิจัยด้าน Artificial Intelligence (AI) ของพี่นอตได้รับรางวัลงานวิจัยดีเยี่ยมจาก สำนักงานคณะกรรมการวิจัยแห่งชาติในปี 2557
ตัวอย่างการสอน โดยพี่นอต
Math Magic















