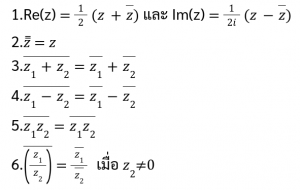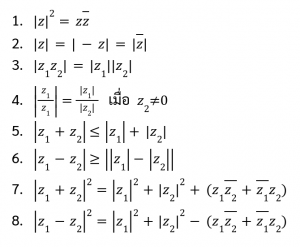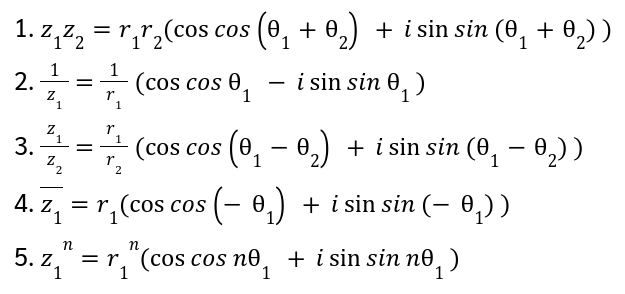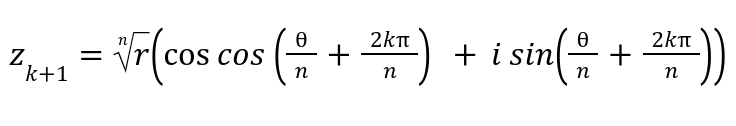PANYA SOCIETY
จำนวนเชิงซ้อน
สรุปเนื้อหาที่สำคัญ
จำนวนเชิงซ้อน เป็นบทแรกเนื้อหา คณิตศาสตร์ ม.5 เทอม 2 โดยอาศัยพื้นฐานมาจากเนื้อหา ฟังก์ชันตรีโกณมิติ ของคณิตศาสตร์ ม.5 เทอม 1 ทำให้น้องๆควรมีพื้นฐานของ ฟังก์ชันตรีโกณมิติ ในการทำความเข้าใจเนื้อหาของส่วนนี้ และจำนวนเชิงซ้อนนี้มักถูกพบเห็บได้บ่อยๆในข้อสอบ A – Level ทำให้น้องๆควรเป็นอย่างยิ่งในการทำความเข้าใจเนื้อหาของส่วนนี้ เพื่อเก็บคะแนนมาให้ได้
เนื้อหาหลักของบทนี้ประกอบด้วย รายละเอียดบทย่อย ดังนี้
- หน่วยจินตภาพ
- สมบัติเชิงพีชคณิตของจำนวนเชิงซ้อน
- สังยุคและค่าสัมบูรณ์ของจำนวนเชิงซ้อน
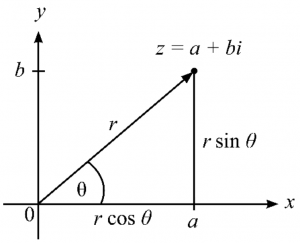
- กราฟของจำนวนเชิงซ้อน
- รูปเชิงขั้วของจำนวนเชิงซ้อน
- รากที่ n ของจำนวนเชิงซ้อน
จำนวนเชิงซ้อน
ให้ i=√-1 เรียกว่า หน่วยจินตภาพ จำนวนเชิงซ้อน คือ จำนวนที่เขียนอยู่ในรูป
z = a+bi หรือ (a,b) โดย a,b เป็นจำนวนจริง
เรียก a ว่า ส่วนจริงของ z(Re(z)) เรียก b ว่า ส่วนจินตภาพของ z(Im(z))
- ถ้าเหลือเศษ 1 : in = i
- ถ้าเหลือเศษ 2 : in = -1
- ถ้าเหลือเศษ 3 : in = -i
- ถ้าหารลงตัว : in = 1
สมบัติของจำนวนเชิงซ้อน
- เอกลักษณ์การบวก คือ 0
- เอกลักษณ์การคูณ คือ 1
- อินเวอร์สการบวกของ z คือ –z
- อินเวอร์สการคูณของ z คือ z-1 = 1⁄z
สังยุคและค่าสัมบูรณ์ของจำนวนเชิงซ้อน
z = a – bi
สมบัติของสังยุคของจำนวนเชิงซ้อน
ให้ z = a + bi ค่าสัมบูรณ์ของ z เขียนแทนด้วย |z|
|z| = √a² + b²
สมบัติของค่าสัมบูรณ์ของจำนวนเชิงซ้อน
ให้ z = a + bi จะเขียน z บนระนาบเชิงซ้อนได้ดังนี้
รูปชิงขั้วของ z เขียนได้เป็น
z = r(cos cos θ + i sin sin θ)
โดยที่ r = √a² + b² = |z| และ tanθ = b⁄a
สมบัติของรูปเชิงขั้วของจำนวนเชิงซ้อน
รากที่ n ของจำนวนเชิงซ้อน จะมี n ราก
โดยที่ k = 0, 1, 2, …, n-1
zk+1 เป็นรากที่ n ของ z
คุยกันท้ายบท
1. ถ้า z เป็นจำนวนเชิงซ้อน ซึ่งสอดคล้องกับสมการ z + |z-1⁄z-1| = -3 + 2i แล้ว |z| มีค่าเท่ากับข้อใดต่อไปนี้ (สามัญ1 ปี’59)
- 3
- √10
- √13
- 2√5
- 4
2. ถ้ากำหนดให้ P(x) เป็นพหุนามดีกรี 4 ซึ่งมีสัมประสิทธิ์เป็นจำนวนจริง และสัมประสิทธิ์ของ x4 เท่ากับ 1 ถ้า z1 และ z2 เป็นรากที่ 2 ของ 2i และเป็นคำตอบของสมการ P(x) = 0 ด้วย แล้ว P(1) มีค่าเท่ากับข้อใดต่อไปนี้ (สามัญ ปี’56)
- 3
- 5
- 7
- 9
- 10
น้องๆคงได้รับความรู้เรื่อง “จำนวนเชิงซ้อน” พร้อมกับใช้ความรู้พื้นฐานมาจากเนื้อหาฟังก์ชันตรีโกณมิติที่ผ่านมาจากคณิตศาสตร์ ม.5 เทอม 1 และจำนวนเชิงซ้อนนี้เองก็จะถูกนำไปใช้ต่อในบทถัดไปในเรื่องของ “หลักการนับเบื้องต้น” ทำให้เห็นได้ว่า น้องๆจำเป็นอย่างยิ่งในการทำความเข้าใจในเนื้อหาอย่างต่อเนื่องเพราะแต่ละส่วนนั้นเป็นส่วนสำคัญในการต่อยอดของการเรียนในบทถัดๆไป
พี่หวังว่า น้องๆจะสนุกกับการเรียนคณิตศาสตร์ ม.5 เทอม 2 ไปตลอดทั้งเทอม และขอให้น้องๆประสบความสำเร็จในการเรียนเทอมนี้ ได้เกรดดังหวัง คะแนนปังทุกคนเลยครับ แล้วพบกันในบทความสรุปเนื้อหาคณิตศาสตร์ ม.5 เทอม 2 บทถัดไปนะครับ
คณิตศาสตร์ ม.5 เทอม 2 - จำนวนเชิงซ้อน
- ทำงานตำแหน่ง Software Engineer ที่ Google กว่า 10 ปี
- ได้รับทุนเล่าเรียนหลวงไปศึกษาระดับปริญญาตรี ด้าน Electrical and Computer Engineering และ Computer Science ที่ Carnegie Mellon University สหรัฐอเมริกา
- จบปริญญาเอก ด้าน Artificial Intelligence พร้อมรางวัลนักเรียนดีเด่นจาก UCLA
- ผลงานวิจัยด้าน Artificial Intelligence (AI) ของพี่นอตได้รับรางวัลงานวิจัยดีเยี่ยมจาก สำนักงานคณะกรรมการวิจัยแห่งชาติในปี 2557
ทำความรู้จัก พี่นอต (ดร.ธรรมนิติ์ พิพัฒน์ศรีสวัสดิ์)
Math Magic
