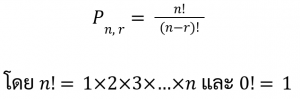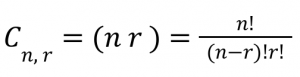สรุปเนื้อหาที่สำคัญ
กลับมากันอีกครั้งสำหรับสรุปเนื้อหาวิชา คณิตศาสตร์ มัธยมปลาย ระดับชั้น ม.5 เทอม 2 ในเรื่อง “หลักการนับเบื้องต้น” และแน่นอนอย่างที่พี่นอตเคยได้เกรินไปในตอนท้ายของบทที่แล้วว่าบทนี้นั้นจะใช้ความรู้พื้นฐานมาจากเนื้อหาของ “จำนวนเชิงซ้อน”
ดังนั้น ถ้าน้องๆคนไหนที่ยังไม่เข้าใจเนื้อหาของ “จำนวนเชิงซ้อน” พี่นอตอยากให้ลองย้อนกลับไปอ่านบทความก่อนหน้านี้ที่พี่นอตเคยได้เขียนไว้แล้วนะครับ เพื่อเป็นการเตรียมพื้นฐานในการทำความเข้าใจเนื้อหา “หลักการนับเบื้องต้น” ส่วนน้องๆคนไหนเตรียมตัวมาพร้อมแล้วเรามาลุยกันเลย แล้วอย่าลืมลองทำแบบฝึกหัดท้ายบทที่พี่แนบไว้ด้วยนะครับ ขอให้เทอมนี้ คณิตศาสตร์ ม.5 เทอม 2 เกรดปังๆเลยนะ ติดตามเนื้อหาไปด้วยกันครับ 🙂
โดยเนื้อหาหลักของบทนี้จะประกอบด้วยรายละเอียดบทย่อย ดังนี้
- หลักการบวกและหลักการคูณ
- การเรียงสับเปลี่ยน
- การจัดหมู่
- ทฤษฎีบททวินาม
หลักการบวกและหลักการคูณ
ในการที่เราจะนับจำนวนสิ่งของ เหตุการณ์ หรือจำนวนวิธีในการทำงานบางอย่าง อาจจะสามารถนับได้โดยตรงจากการค่อยๆ ไล่นับไปจนครบ แต่หากสิ่งที่จะนับมีจำนวนมาก อาจจะทำให้การนับโดยตรงนั้นทำได้ยาก จึงมีหลักการนับสิ่งต่างๆ เบื้องต้น เพื่อช่วยให้การนับสิ่งที่มีจำนวนเยอะๆ ทำได้ง่ายขึ้น โดยแบ่งเป็น
ถ้าสามารถแบ่งการทำงานออกเป็นหลายกรณี จำนวนวิธีการทำงานทั้งหมด คือ ผลรวมของจำนวนวิธีการทำงานทุกกรณี แสดงออกมาในรูปแบบ
n1 + n2 + … + nn
ตัวอย่างเช่น มีการบ้านวิชาคณิตศาสตร์ 2 ชิ้น วิชาภาษาอังกฤษ 3 ชิ้น และวิชาภาษาไทย 1 ชิ้น จะมีการบ้านให้เลือกทำกี่วิธี?วิธีทำ
- มีการบ้านวิชาคณิตศาสตร์ 2 ชิ้น
- มีการบ้านวิชาภาษาอังกฤษ 3 ชิ้น
- มีการบ้านวิชาภาษาไทย 1 ชิ้น
ถ้าการทำงานแบ่งออกเป็นหลายขั้นตอน จำนวนวิธีการทำงานทั้งหมด คือผลคูณของจำนวนวิธีการทำงานทุกขั้นตอน แสดงออกมาในรูปแบบ
n1 ✕ n2 ✕ … ✕ nn
ตัวอย่างเช่น มีการบ้านวิชาคณิตศาสตร์ 2 ชิ้น วิชาภาษาอังกฤษ 3 ชิ้น และวิชาภาษาไทย 1 ชิ้น ถ้าวันนี้จะเลือกทำการบ้าน 2 ชิ้น โดยเมื่อทำการบ้านชิ้นแรกเสร็จ จะทำชิ้นที่ 2 ต่อ จะมีวิธีทำการบ้านในวันนี้กี่วิธี?
วิธีทำ
- มีการบ้านทั้งหมด 6 ชิ้น
- ขั้นตอนที่ 1 เลือกทำการบ้านชิ้นที่ 1 ซึ่งจะเป็นชิ้นใดก็ได้ มี 6 วิธี
- ขั้นตอนที่ 2 เลือกทำการบ้านชิ้นที่ 2 ต่อ โดยเลือกจากการบ้านชิ้นที่เหลือ มี 5 วิธี
ดังนั้น จะมีวิธีทำการบ้านในวันนี้ 6 ✕ 5 = 30 วิธี
การเรียงสับเปลี่ยน
ต่อเนื่องจากหลักการคูณ หากมีสิ่งของอยู่ n ชิ้นที่แตกต่างกันทั้งหมด แล้วต้องการจะนำสิ่งของ r ชิ้นจากสิ่งของที่มีอยู่ นำมาเรียงลำดับจะได้ว่า
- ขั้นตอนที่ 1 เลือกของชิ้นที่ 1 มาวาง ซึ่งจะเป็นชิ้นใดก็ได้ มี n ชิ้น
- ขั้นตอนที่ 2 เลือกของชิ้นที่ 2 มาวาง โดยเป็นชิ้นที่เหลือจากการวางชิ้นที่ 1 มี n-1 ชิ้น
.
.
.
- ขั้นตอนที่ r เลือกของชิ้นที่ r โดยเป็นชิ้นที่เหลือจากการวางชิ้นที่ r-1 มี n-r+1 ชิ้น
ดังนั้น จำนวนวิธีในการนำสิ่งของมาเรียง = n ✕ (n-1) ✕ (n-2) ✕ … ✕ (n-r+1)
หรือเรียกอีกอย่างว่า แฟกทอเรียล เขียนแทนด้วย n! โดยที่ n เป็นจำนวนเต็มบวก
โดย n! = n ✕ (n-1) ✕ (n-2) ✕ … ✕ 3 ✕ 2 ✕ 1
และ 0! = 1 *ระวังโดนหลอกกันนะครับน้องๆ*
การเรียงสับเปลี่ยนแบ่งออกเป็นอีก 3 อย่างด้วยกัน คือ
การเรียงสับเปลี่ยนสิ่งของที่แตกต่างกันทั้งหมด
มีสิ่งของ n ชิ้น ที่ไม่ซ้ำกัน ต้องการนำมาเรียง r ชิ้น จะมีจำนวนวิธีเรียง คือ
ตัวอย่าง มีเลขโดด 5 ตัว คือ 1, 4, 6, 7, 9 จะนำมาสร้างเป็นเลข 5 หลักได้กี่จำนวน
วิธีทำ วิธีเรียงลำดับตัวเลขทั้ง 5 ตัว โดยนำมาเรียงทั้งหมด คือ P5,5 = 5! = 120 วิธี
การเรียงสับเปลี่ยนสิ่งของที่ไม่แตกต่างกันทั้งหมด
มีสิ่งของ n ชิ้น โดยมีสิ่งของเหมือนกัน k กลุ่ม นำมาเรียงสับเปลี่ยน จะมีจำนวนวิธีเรียง คือ
ตัวอย่าง ต้องการนำตัวอักษรคำว่า “coffee” มาเรียงใหม่โดยไม่สนใจความหมาย จะเรียงได้กี่วิธี
วิธีทำ มีตัวอักษร f ซ้ำ 2 ตัว, e ซ้ำ 2 ตัว, c,o อย่างละ 1 ตัว
ดั้งนั้นจะเรียงได้ 6!⁄2!✕2!✕1!✕1! = 180 วิธี
จะเห็นได้ว่าสามารถพิจารณาเพียงตัวที่ซ้ำได้
การเรียงสับเปลี่ยนสิ่งของที่แตกต่างกันทั้งหมดเชิงวงกลม
มีสิ่งของ n ชิ้น ที่ไม่ซ้ำกัน นำมาเรียงเป็นวงกลม จะมีจำนวนวิธีเรียง คือ
(n-1)!
ตัวอย่าง มีดอกไม้อยู่ 10 ดอก ที่แตกต่างกัน ต้องการนำดอกไม้ทั้ง 10 ดอกนี้มาร้อยเป็นพวงมาลัย จะร้อยพวงมาลัยได้กี่แบบ
วิธีทำ การร้อยพวงมาลัย ถือเป็นเรียงดอกไม้เป็นวงกลม ดังนั้นจะร้อยพวงมาลัยได้ (10-1)! = 9! = 362,880 แบบ
การจัดหมู่
การจัดหมู่ คือ การเลือกกลุ่มของสิ่งของมา โดยไม่คำนึงถึงลำดับในการเรียงของสิ่งของในกลุ่มที่เลือกมา หากกลุ่มใดมีสิ่งของในกลุ่มเหมือนกัน จะนับเป็นการจัดหมู่เพียง 1 วิธี เช่น การจัดกลุ่ม 3 คน เพื่อทำงานกลุ่ม กลุ่ม A มีสมาชิกคือ พลอย แป๊ก และหยา จะเห็นได้ว่า ถ้าเราเรียงสมาชิกใหม่เป็น หยา แป๊ก และพลอย, แป๊ก หยา และพลอย หรือเรียงแบบอื่นๆก็จะนับเพียงว่า พลอย แป๊ก และหยา อยู่กลุ่มเดียวกัน
การจัดหมู่สิ่งของที่แตกต่างกันทั้งหมด
มีสิ่งของ n ชิ้น ที่ไม่ซ้ำกัน ต้องการเลือกมา r ชิ้น จะมีจำนวนวิธีจัดหมู่ คือ
ตัวอย่าง ร้านไอศกรีมร้านหนึ่ง มีไอศกรีมอยู่ 6 รส แพรวต้องการสั่งไอศกรีม 2 รส จากร้านนี้ แพรวจะสั่งได้ทั้งหมดกี่วิธี
วิธีทำ เลือกไอศกรีม 2 จากทั้งหมด 6 รส (62) = 6!⁄(6-2)!2! = 15 วิธี
ทฤษฎีบททวินาม
ในการกระจาย x + yn เมื่อ x และ y เป็นจำนวนจริง และ n เป็นจำนวนเต็มบวก สามารถทำได้โดยนำ x หรือ y ของวงเล็บแรกเลือกคูณกับ x หรือ y ของวงเล็บต่อๆไป จนถึงวงเล็บที่ n จะได้ออกมา 1 พจน์ แล้วทำซ้ำไปเรื่อยๆ จนครบทุกวิธี โดยวิธีในการเลือกแต่ละพจน์ต้องแตกต่างกัน แล้วจึงค่อยนำทุกพจน์มาบวกกัน แสดงอยู่ในรูปแบบดังนี้
(x + y)n = (n 0)xn + (n 1)xn-1y +…+ (n r)xn-ryr +…+ (n n)yn
ตัวอย่าง จงกระจาย (x – y)3
วิธีทำ (x – y)3 = (3 0)x3 + (3 1)x2(-y) + (3 2)x(-y)2 + (3 3)(-y)3 = x3 – 3x2y + 3xy2 – y3
คุยกันท้ายบท
1. ในการจัดเด็ก 7 คน ซึ่งมีอายุ 1,2,3,4,5,6,7 ขวบ นั่งเก้าอี้ 7 ตัว ซึ่งติดหมายเลข 1,2,3,4,5,6,7 โดยกำหนดให้เด็กที่จะนั่งเก้าอี้หมายเลข k ต้องมีอายุมากกว่าหรือเท่ากับ k-1 ขวบ จะมีวิธีในการจัดเท่ากับข้อใดต่อไปนี้ (สามัญ ปี’55)
- 32
- 60
- 64
- 120
- 128
2. มีข้อสอบปรนัย 20 ข้อ คะแนนเต็ม 50 คะแนน โดยกำหนดข้อ 1-10 ข้อละ 4 คะแนน และข้อ 11-20 ข้อละ 1 คะแนน หากนักเรียนตอบข้อใดถูก จะได้คะแนนเต็มของข้อนั้น แต่ถ้าตอบผิดหรือไม่ตอบจะได้ 0 คะแนน จะมีกี่วิธีที่นักเรียนคนหนึ่ง จะทำข้อสอบชุดนี้ได้คะแนนรวม 45 คะแนน (PAT1 ก.ค. ’53)
เป็นยังไงกันบ้างครับกับเนื้อหาและแบบฝึกหัดของ “หลักการนับเบื้องต้น” น้องๆจะเห็นได้ว่ามีการนำเนื้อหาของ “จำนวนเชิงซ้อน” มาใช้ในบทนี้ด้วย ซึ่งถ้าน้องคนไหน ไม่มีความรู้ความเข้าใจที่แท้จริงจากบทที่แล้ว ก็จะยิ่งสร้างปมปัญหาต่อมาถึงบทนี้ และรวมไปถึงบทถัดไปด้วยซึ่งก็คือ “ความน่าจะเป็น” นั้นเอง รับรองเลยว่าใครที่ชอบเสี่ยงดวงหรือเสี่ยงโชคนั้นจะต้องชอบกับเนื้อหาในบทถัดไปอย่างแน่นอน ฮ่าๆ
ซึ่งจากสถิติที่ผ่านเนื้อหาในส่วนของหลักการนับเบื้องต้น และความน่าจะเป็นมักจะถูกรวมกันนำไปออกข้อสอบ A – Level ประมาณ 3-4 ข้ออยู่เป็นประจำ ดังนั้นถ้าน้องๆได้ลองทำแบบฝึกหัดท้ายบทที่พี่นอตได้แนบไว้ น้องๆน่าจะเก็บคะแนนจากส่วนนี้ได้ไม่ยากอย่างแน่นอน แต่ถ้าน้องๆคนไหนอยากได้เนื้อหาที่ละเอียดมากกว่านี้ รวมไปถึงแบบฝึกหัดที่เข้มข้นกว่านี้ พี่นอตขอแนะนำคอร์สวิชา “คณิตศาสตร์ ม.5 เทอม 2” จาก Panya Society ที่มีการปูพื้นฐานตั้งแต่ง่ายไปจนถึงระดับยาก เน้นความเข้าใจ ไม่เน้นกาารท่องจำ พร้อมทั้งแบบฝึกหัด รวมไปถึงตัวอย่างข้อสอบจากข้อสอบจริงในการสอบเข้าระดับมหาวิทยาลัย A – Level
สุดท้ายนี้พี่นอตหวังว่า น้องๆจะสนุกกับการเรียนคณิตศาสตร์ ม.5 เทอม 2 ไปตลอดทั้งเทอม และขอให้น้องๆประสบความสำเร็จในการเรียนเทอมนี้ ได้เกรดดังหวัง คะแนนปังกันทุกคนเลยนะครับ แล้วพบกันในบทความสรุปเนื้อหาคณิตศาสตร์ ม.5 เทอม 2 บท “ความน่าจะเป็น” รับรองว่าสนุกแน่นอน
คณิตศาสตร์ ม.5 เทอม 2 - หลักการนับเบื้องต้น
- อดีต Senior Software Engineer ที่ Google กว่า 10 ปี
- ได้รับทุนเล่าเรียนหลวงไปศึกษาระดับปริญญาตรี ด้าน Electrical and Computer Engineering และ Computer Science ที่ Carnegie Mellon University สหรัฐอเมริกา
- จบปริญญาเอก ด้าน Artificial Intelligence พร้อมรางวัลนักเรียนดีเด่นจาก UCLA
- ผลงานวิจัยด้าน Artificial Intelligence (AI) ของพี่นอตได้รับรางวัลงานวิจัยดีเยี่ยมจาก สำนักงานคณะกรรมการวิจัยแห่งชาติในปี 2557
ทำความรู้จัก พี่นอต (ดร.ธรรมนิติ์ พิพัฒน์ศรีสวัสดิ์)
Math Magic