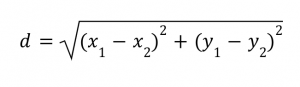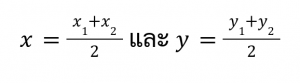สรุปเนื้อหาที่สำคัญ
แล้วเราก็เดินทางมาสู่บทที่ 3 ของการสรุปเนื้อหาวิชาคณิตศาสตร์ ม. 4 เทอม 2 “เรขาคณิตวิเคราะห์ และภาคตัดกรวย” เป็นบทสุดท้ายของการเรียนวิชาคณิตศาสตร์ในเทอม 2 ในบทนี้น้องๆได้สนุกกับการเรียนรู้วิชาเลขที่มี “ภาพของกราฟ” อันหลากหลายให้น้องๆได้สนุกกับการทำโจทย์ครับ
จากสถิติที่ผ่านมา การออกข้อสอบเข้าระดับมหาวิทยาลัย TCAS เนื้อหาในส่วนนี้ก็มักจะปรากฏให้เห็นอยู่ประมาณ 3 ข้อเป็นประจำ ใน A – Level แสดงให้เห็นว่า คณิตศาสตร์ ม.4 เทอม 2 เรื่อง “เรขาคณิตวิเคราะห์ และภาคตัดกรวย” นั้นมีความสำคัญไม่แพ้บทอื่นๆ น้องๆควรจะต้องทำความเข้าใจเนื้อหา และพื้นฐานของบทนี้ให้แน่น เพื่อพร้อมรับมือในการทำข้อสอบ และคว้าคะแนนจากบทนี้มาให้ได้
และน้องๆที่มีความสนใจในเรื่องรูป การวาดกราฟ และความเชื่อมโยงของสมการ และรูปกราฟ น่าจะเป็นอีกบทที่เรียนก็สนุก และทำโจทย์ก็ได้เชาว์ปัญญาไปด้วย สร้างทักษะให้กับน้องๆในการอ่านกราฟมากยิ่งขึ้นด้วยครับผม
เนื้อหาหลักของบทนี้ประกอบด้วย รายละเอียดบทย่อย ดังนี้
- ความรู้เบื้องต้นเกี่ยวกับเรขาคณิตวิเคราะห์
- ระยะทางระหว่างจุดสองจุด
- จุดกึ่งกลางระหว่างจุดสองจุด
- ความชันของเส้นตรง
- เส้นขนาน
- เส้นตั้งฉาก
- ความสัมพันธ์ซึ่งมีกราฟเป็นเส้นตรง
- ระยะห่างระหว่างเส้นตรงกับจุด
- ภาคตัดกรวย
- วงกลม
- วงรี
- พาราโบลา (Parabola)
- ไฮเพอร์โบลา (Hyperbola)
- การเลื่อนกราฟ
เรขาคณิตวิเคราะห์
บทนี้จะศึกษาเกี่ยวกับจุดและรูปทรงต่าง ๆ ใน 2 มิติ โดยเริ่มจาก
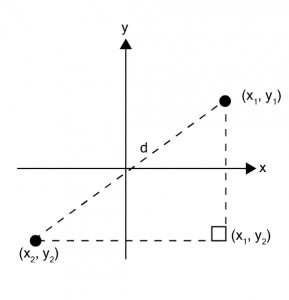
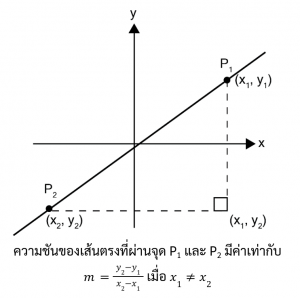
ระยะห่างระหว่างจุด ให้จุด (x1, y1) และ (x2, y2) อยู่บนระนาบ x – y ดังรูป
ระยะห่างระหว่างจุด (x1, y1) และ (x2, y2) จะหาได้จากการใช้ทฤษฎีบทพีทาโกรัส ได้ว่า
ข้อสังเกต
- ถ้า x1 = x2 แสดงว่า จุดทั้งสองอยู่ในแนวเส้นตรงที่ขนานกับแกน y
จึงได้ว่า ระยะห่างระหว่างสองจุดนั้น = |y1 – y2| - ถ้า y1 = y2 แสดงว่า จุดทั้งสองอยู่ในแนวเส้นตรงที่ขนานกับแกน x
จึงได้ว่า ระยะห่างระหว่างสองจุดนั้น = |x1 – x2|
ตัวอย่างโจทย์ จงหาระยะห่างระหว่าจุด (1,2) และ (4,6) เฉลย
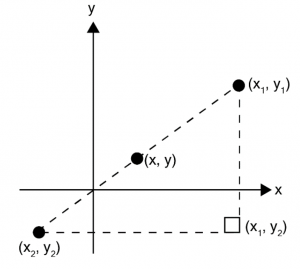
จุดกึ่งกลางระหว่างสองจุด ถ้าจุด (x, y) เป็นจุดกึ่งกลางระหว่างจุด (x1, y1) และ (x2, y2) ดังรูป
แสดงว่า x เป็นค่ากึ่งกลางของ x1 และ x2 และ y เป็นค่ากึ่งกลางของ y1 และ y2 จะได้ว่า
ความชันของเส้นตรง
ข้อสังเกต
- ถ้าความชันเป็นบวก เส้นตรงจะทำมุมแหลมกับแกน x เมื่อวัดมุมทวนเข็มนาฬิกา
- ถ้าความชันเป็นลบ เส้นตรงจะทำมุมป้านกับแกน x เมื่อวัดมุมทวนเข็มนาฬิกา
- ถ้า x1 = x2 เส้นตรงจะขนานกับแกน y ซึ่งความชันจะหาค่าไม่ได้
- ถ้า y1 = y2 เส้นตรงจะขนานกับแกน x ซึ่งความชันจะเท่ากับศูนย์
ตัวอย่างโจทย์ จงหาความชันของเส้นตรงที่ผ่านสองจุดต่อไปนี้ (-7, -3) และ (-13, -6) เฉลย
เส้นขนานและเส้นตั้งฉาก
- เส้นตรงที่ไม่ขนานกับแกน y จะขนานกันก็ต่อเมื่อมีความชันเท่ากัน
- เส้นตรงที่ขนานกับแกน y จะขนานกับเส้นตรงที่ขนานกับแกน y เส้นอื่น ๆ ด้วย
- เส้นตรงที่ไม่ขนานกับแกน y จะตั้งฉากกันก็ต่อเมื่อมีความชันคูณกันได้เท่ากับ -1
- เส้นตรงที่ขนานกับแกน y จะตั้งฉากกับเส้นตรงที่ขนานแกน x
ความสัมพันธ์ซึ่งมีกราฟเป็นเส้นตรง
ให้ (x, y) เป็นจุดใด ๆ บนเส้นตรงที่ไม่ขนานกับแกน y และลากผ่านจุด (x1, y1) และ (x2, y2)
จะได้สมการเส้นตรงนี้ คือ
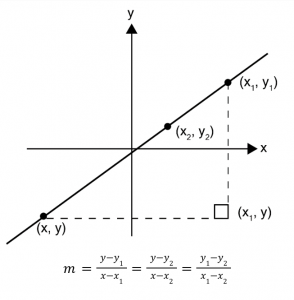
ถ้าให้เส้นตรงที่มีความชัน m ตัดแกน y ที่จุด (0, c) จะมีสมการเส้นตรง คือ
y = mx + c
เรียก c ว่าระยะตัดแกน y
และจะได้จุดตัดแกน x คือจุดที่ y = 0 จะได้ว่า
0 = mx+c
x = (-c/m)
ดังนั้น จุดตัดแกน x คือ ((-c/m), 0)
เรียก (-c/m) ว่าระยะตัดแกน x
ข้อสังเกต
- สมการเส้นตรงที่ขนานกับแกน x จะมีสมการเป็น y = c โดยที่ c เป็นค่าคงที่ใด ๆ
- สมการเส้นตรงที่ขนานกับแกน y จะมีสมการเป็น x = k โดยที่ k เป็นค่าคงที่ใด ๆ
- เราสามารถหาสมการเส้นตรงใด ๆ ที่ไม่ขนานกับแกน y ได้ จากการแก้สมการ หรือระบบสมการ ของสมการเส้นตรง y = mx + c จากเงื่อนไขที่กำหนดมา
- ถ้าเส้นตรงผ่านจุด (a, b) แสดงว่าจุด (a, b) อยู่บนเส้นตรงนั้น จะได้ว่า b = ma + c
โจทย์ตัวอย่าง จงหาสมการเส้นตรงที่มีความชันเท่ากับ -7 และผ่านจุด (0, -5) เฉลย
ภาคตัดกรวย
บทนี้จะเรียนเกี่ยวกับรูปร่างต่าง ๆ ที่เกิดจากการตัดทรงกรวยด้วยระนาบหนึ่ง โดยการตัดทำมุมต่าง ๆ กัน จะทำให้ได้รอยเฉือนรูปร่างต่าง ๆ ได้แก่ วงกลม, วงรี, พาราโบลา และไฮเพอร์โบลา
ซึ่งคุณสมบัติของรูปร่างต่าง ๆ เหล่านี้ สามารถนำไปประยุกต์ใช้ในชีวิตประจำวันได้ โดยเฉพาะในทางวิทยาศาสตร์ และดาราศาสตร์
วงกลม
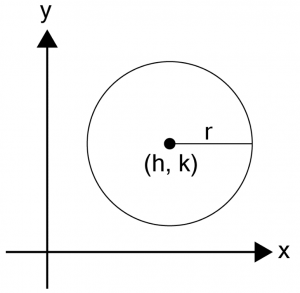
นิยามของวงกลม คือ เซตของจุดที่มีระยะห่างจากจุด ๆ หนึ่ง (จุดศูนย์กลางของวงกลม) เป็นระยะเท่า ๆ กัน จะได้ว่า ทุก ๆ จุดบนวงกลมจะมีระยะห่างจากจุดศูนย์กลางเท่ากับรัศมี
สมการวงกลม กลมที่มีจุดศูนย์กลางอยู่ที่จุด (h, k) และมีรัศมียาว r หน่วย จะมีสมการ คือ
(x – h)2 + (y – k)2 = r2
แต่สมการวงกลมสามารถเขียนได้อีกแบบดังนี้
จาก (x-h)2 + (y-k)2 = r2
จะได้ x2 – 2hx + h2 + y2 – 2ky + y2 = r2
x2 + y2 – 2hx – 2ky + h2 + y2 – r2 = 0
ให้ A = -2h, B = -2k, C = h2 + k2 – r2
จะได้รูปทั่วไปของสมการวงกลม คือ x2 + y2 + Ax + By + C = 0
วงรี
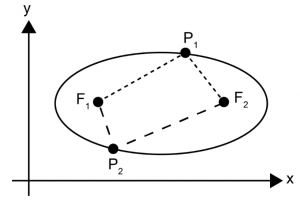
นิยามของวงรี ให้ F1 และ F2 เป็นจุดใด ๆ จุด P ใด ๆ บนวงรีจะมีผลบวกของระยะจากจุดนั้นไปยังจุด F1 และ F2 เป็นค่าคงที่ค่าหนึ่งเสมอ โดยที่ค่าคงที่นี้มีค่ามากกว่าระยะ F1F2 หรือก็คือ F1P + F2P = k โดยที่ k > F1F2 สำหรับทุกจุด P บนวงรี เรียกจุด F1 และ F2 ว่า จุดโฟกัส และเรียก k ว่า ผลบวกคงตัว
F1P1 + F2P1 = k = F1P2 + F2P2
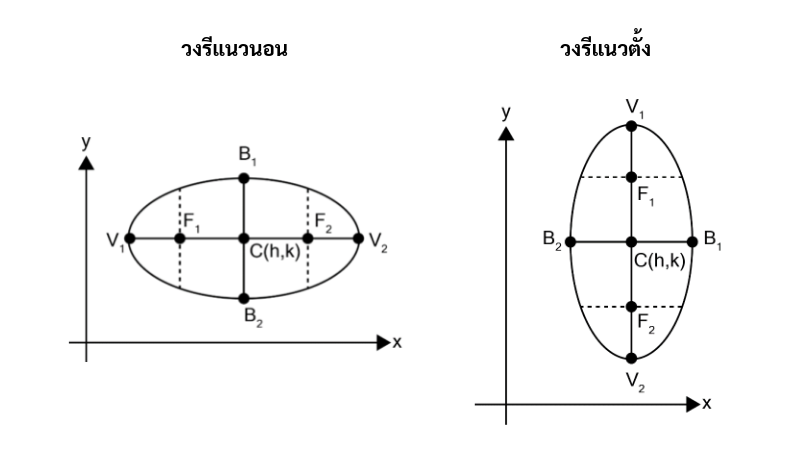
ส่วนประกอบของวงรี กราฟวงรีที่จะศึกษาในตอนนี้มี 2 แบบ ดังนี้
ส่วนประกอบของวงรี มีดังนี้
1. จุดศูนย์กลางวงรี (จากรูปคือจุด C(h, k)) คือ จุดกึ่งกลางระหว่างจุดโฟกัสทั้งสองจุด กำหนดให้ จุดโฟกัสทั้งสองห่างจากจุดศูนย์กลาง c หน่วย จะได้ว่า จุดโฟกัสทั้งสองห่างกัน 2c หน่วย
- ถ้าวงรีเป็นแนวนอน จะได้ว่าจุดโฟกัสคือ (h ± c, k)
- ถ้าวงรีเป็นแนวตั้ง จะได้ว่าจุดโฟกัสคือ (h, k ± c)
2. แกนเอก (จากรูปคือเส้นตรง V1,V2) คือ ส่วนของเส้นตรงที่มีจุดปลายอยู่บนวงรี และลากผ่านจุดโฟกัสทั้งสองจุด กำหนดให้ แกนเอกยาว 2a หน่วย
3. จุดยอดของวงรี (จากรูปคือจุด V1 และ V2) คือ จุดปลายของแกนเอก
จะเห็นว่า ผลบวกคงตัว จะมีค่าเท่ากับความยาวแกนเอก = 2a หน่วย
- ถ้าวงรีเป็นแนวนอน จะได้ว่าจุดยอดคือ (h ± a, k)
- ถ้าวงรีเป็นแนวตั้ง จะได้ว่าจุดยอดคือ (h, k ± a)
- จุดกึ่งกลางระหว่างจุดยอดทั้งสองจุด คือ จุดศูนย์กลางวงรี
4. แกนโท (จากรูปคือเส้นตรง B1B2) คือ ส่วนของเส้นตรงที่มีจุดปลายอยู่บนวงรี โดยตั้งฉากกับแกนเอก
และผ่านจุดศูนย์กลางวงรี กำหนดให้ แกนโทยาว 2b หน่วย ดังนั้น จุดกึ่งกลางระหว่างจุดปลายของแกนโท คือ จุดศูนย์กลางวงรี
5. เส้นเลตัสเรกตัม (Latus Rectum) (คือ เส้นประทั้งสองเส้น ในรูปวงรีแนวนอน และวงรีแนวตั้ง) คือ ส่วนของเส้นตรงที่มีจุดปลาย อยู่บนวงรี(คอร์ดของวงรี) โดยตั้งฉากกับแกนเอก และผ่านจุดโฟกัส
6. ค่าความเยื้องศูนย์กลางของวงรี (e) คือ ค่าที่บอกความรีของวงรี โดย e = c/a
- ค่า e มีค่าอยู่ในช่วง (0, 1)
- ถ้า e มีค่าเข้าใกล้ 1 วงรีจะรีมาก
- ถ้า e มีค่าเข้าใกล้ 0 วงรีจะรีน้อย
สมการวงรี
โจทย์ตัวอย่าง วงรีที่มีสมการเป็น (x+1)2⁄25 + (y+2)2⁄16 = 1
- เป็นวงรีแนวนอน หรือแนวตั้ง ?
- หาจุดศูนย์กลางวงรี ?
- จุดโฟกัส ความยาวแกนเอก ?
- จุดยอดของวงรี ?
- ความยาวแกนโท ?
- ความยาวของเส้นเลตัสเรกตัม ?
- ค่าความเยื้องศูนย์กลางของวงรีนี้ ? เฉลย
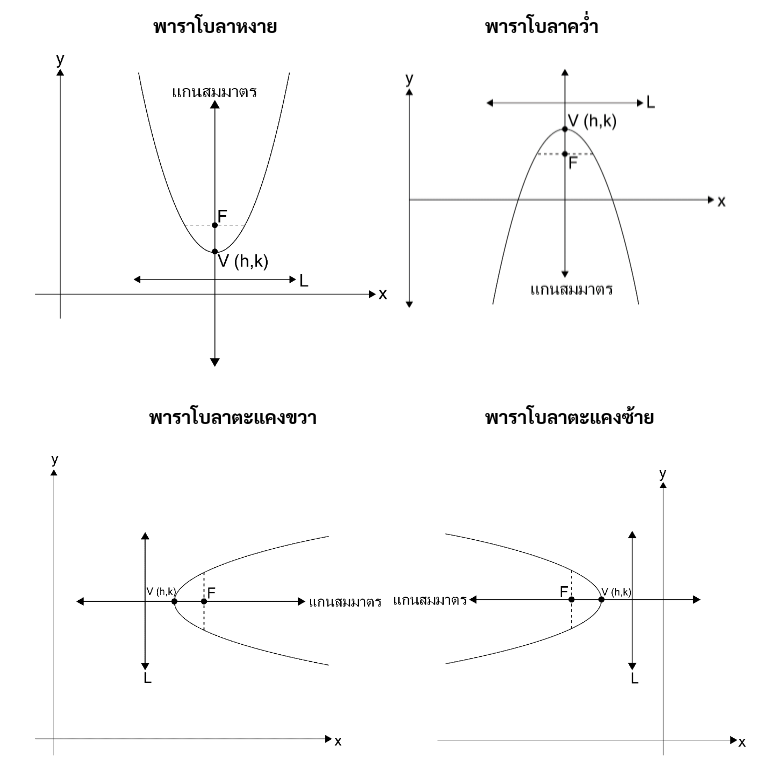
พาราโบลา
นิยามของพาราโบลา ให้ L เป็นเส้นตรงใด ๆ และ F เป็นจุดใด ๆ ที่ไม่อยู่บนเส้นตรง L จุด P ใด ๆ บนพาราโบลาจะมีระยะห่างจากเส้นตรง L เท่ากับ ระยะห่างจากจุด F เรียกจุด F ว่า จุดโฟกัสของพาราโบลา และเรียกเส้นตรง L ว่า เส้นไดเรกตริกซ์
ส่วนประกอบของพาราโบลา
กราฟพาราโบลาที่จะศึกษามี 4 แบบ ดังนี้
ส่วนประกอบของพาราโบลา มีดังนี้
1. จุดยอด (จากรูปคือ V(h, k)) คือ จุดที่แบ่งครึ่งส่วนของเส้นตรงที่ลากจากจุดโฟกัสไปตั้งฉากกับเส้นไดเรกตริกซ์ ให้ระยะห่างระหว่างจุดโฟกัสกับจดยอดเท่ากับ a จะได้ระยะห่างระหว่างจุดโฟกัสกับเส้นไดเรกตริกซ์เท่ากับ 2a
2. แกนสมมาตร คือ เส้นตรงที่ตั้งฉากกับเส้นไดเรกตริกซ์ และผ่านจุดโฟกัส และจะผ่านจุดยอดด้วย แกนสมมาตรจะแบ่งกราฟพาราโบลาออกเป็น 2 ส่วนที่สมมาตรกัน
3. เส้นเลตัสเรกตัม (จากรูปคือ เส้นประ) คือ ส่วนของเส้นตรงที่มีจุดปลายอยู่บนพาราโบลา และลากผ่านจุดโฟกัส และขนานกับเส้นไดเรกตริกซ์ เส้นเลตัสเรกตัมยาวเท่ากับ 4a
ตารางแสดงส่วนประกอบของพาราโบลา
| ลักษณะกราฟ | จุดโฟกัส | สมการเส้นไดเรกตริกซ์ | สมการแกนสมมาตร | จุดปลายของเส้นเลตัสเรกตัม |
| หงาย | (h, k + a) | y = k – a | x = h | (h 2a, k + a) |
| คว่ำ | (h, k – a) | y = k + a | x = h | (h 2a, k – a) |
| ตะแคงขวา | (h + a, k) | x = h – a | y = k | (h + a, k 2a) |
| ตะแคงซ้าย | (h – a, k) | x = h + a | y = k | (h – a, k 2a) |
สมการของพาราโบลา
- พาราโบลาหงาย จะมีสมการ คือ (x – h)2 = 4a(y – k)
- พาราโบลาคว่ำ จะมีสมการ คือ (x – h)2 = -4a(y – k)
- พาราโบลาตะแคงขวา จะมีสมการ คือ (y – k)2 = 4a(x – h)
- พาราโบลาตะแคงซ้าย จะมีสมการ คือ (y – k)2 = -4a(x – h)
โจทย์ตัวอย่าง จงบอกลักษณะกราฟ จุดยอด จุดโฟกัส เส้นไดเรกตริกซ์ แกนสมมาตร ความยาวของเส้นเลตัสเรกตัม และจุดปลายของเส้นเลตัสเรกตัมของพาราโบลาที่มีสมการเป็น y2 = -4x – 4 เฉลย
คุยกันท้ายบท
และนี้ก็คือทั้งหมดของ “เรขาคณิตวิเคราะห์ และภาคตัดกรวย” น้องๆที่อ่านมาจนถึงตรงนี้คงจะเห็นได้ว่าเนื้อหาของคณิตศาสตร์ ม.4 เทอม 2 ทุกๆบทมีความเชื่อมโยงและเป็นพื้นฐานให้กันและกัน ซึ่งถ้าน้องไม่สามารถเข้าใจในพื้นฐานของแต่ละบทก็จะสร้างปัญหาให้แก่บทอื่นๆต่อเนื่องกัน ดังนั้นน้องๆทุกคนควรจะเข้าใจพื้นฐานในทุกๆบทเรียน เพื่อไม่ให้เกิดปัญหาในเวลาการทำข้อสอบ
และอีกสิ่งที่สำคัญก็คือ การทำโจทย์ให้มากๆ จากตัวอย่างที่นอตยกมาให้น้องๆนั้นเป็นส่วนหนึ่งของโจทย์ที่สามารถพบเห็นได้ทั่วไป แต่ถ้าหากใครอยากลองเจอโจทย์ที่ท้าทายมากกว่านี้ พี่นอตอยากให้น้องๆลองเข้ามาเรียนคอร์ส คณิตศาสตร์ ม.4 เทอม 2 จากทาง Panya Society พี่นอตรับรองได้เลยว่ามีตัวอย่างโจทย์ที่ท้าทายมากกว่านี้แน่นอน
สุดท้ายนี้พี่นอตหวังว่า น้องๆจะสนุกกับการเรียนคณิตศาสตร์ ม.4 เทอม 2 ไปตลอดทั้งเทอม ขอให้น้องๆประสบความสำเร็จในการเรียน ได้เกรดดังหวัง คะแนนปังทุกคนเลยครับ แล้วพบกันใหม่ ในบทความชุดต่อไปของพี่นอตนะครับ…
- อดีต Senior Software Engineer ที่ Google กว่า 10 ปี
- ได้รับทุนเล่าเรียนหลวงไปศึกษาระดับปริญญาตรี ด้าน Electrical and Computer Engineering และ Computer Science ที่ Carnegie Mellon University สหรัฐอเมริกา
- จบปริญญาเอก ด้าน Artificial Intelligence พร้อมรางวัลนักเรียนดีเด่นจาก UCLA
- ผลงานวิจัยด้าน Artificial Intelligence (AI) ของพี่นอตได้รับรางวัลงานวิจัยดีเยี่ยมจาก สำนักงานคณะกรรมการวิจัยแห่งชาติในปี 2557
ทำความรู้จัก พี่นอต (ดร.ธรรมนิติ์ พิพัฒน์ศรีสวัสดิ์)