สรุปเนื้อหาที่สำคัญ
และแล้วก็เดินทางกันมาถึงสรุปเนื้อหาวิชาคณิตศาสตร์ มัธยมปลาย ระดับชั้น ม.5 เทอม 2 โดย พี่นอต แห่ง Panya Society ในเรื่อง “ความน่าจะเป็น” ซึ่งเป็นเนื้อหาบทสุดท้ายของวิชาคณิตศาสตร์ ม.5 เทอม 2 กันแล้วนะครับ โดยในบทนี้จะเป็นเนื้อหาที่ต่อยอดมาจากส่วนท้ายของเนื้อหา “หลักการนับเบื้องต้น” และเป็นการใช้อธิบายเหตุการณ์ที่เกิดขึ้นในชีวิตประจำวัน เช่น การออกรางวัล การทอยลูกเต๋า การสุ่มสิ่งของต่างๆ เป็นต้น
ดังนั้น ถ้าน้องๆคนไหนที่ยังไม่ค่อยเข้าใจเนื้อหาของการเรียงสับเปลี่ยน การจัดหมู่ พี่นอตอยากให้น้องๆได้ลองย้อนกลับไปอ่านบทความ “หลักการนับเบื้องต้น” ที่พี่นอตเคยได้เขียนไว้แล้วนะครับ เพื่อเป็นการเตรียมพื้นฐานในการทำความเข้าใจเนื้อหาของ “ความน่าจะเป็น” ส่วนน้องๆคนไหนที่พร้อมแล้วเรามาลุยกันเลย แล้วก็อย่าลืมลองทำแบบฝึกหัดท้ายบทที่พี่แนบไว้ด้วยนะครับ
เนื้อหาหลักของบทนี้ประกอบด้วย รายละเอียดบทย่อย ดังนี้
- การทดลองสุ่ม
- ความน่าจะเป็น
การทดลองสุ่ม
การทดลองสุ่ม คือ การทดลองที่รู้ผลลัพธ์อาจจะเป็นอะไรได้บ้าง แต่ไม่รู้แน่นอนว่าแต่ละครั้งที่ทดลองจะได้ผลลัพธ์เป็นอย่างไร เช่น การทอยลูกเต๋าหนึ่งลูกหนึ่งครั้ง แต้มบนหน้าลูกเต๋าที่อาจจะเป็นได้คือ 1,2,3,4,5,6 แต่บอกไม่ได้แน่นอนว่าแต้มที่จะได้เป็นอะไร
ปริภูมิตัวอย่าง คือ เซตของผลลัพธ์ที่อาจจะเป็นไปได้ทั้งหมดของการทดลองสุ่ม นิยมเขียนแทนด้วย S
เหตุการณ์ คือ เซตของผลลัพธ์ที่เราสนใจจากการทดลองสุ่ม นิยมเขียนแทนด้วย E ดังนั้นจะสังเกตได้ว่า เหตุการณ์จะเป็นสับเซตของปริภูมิตัวอย่างเสมอ
ตัวอย่าง ในการโยนเหรียญ 2 ครั้ง ถ้าผลลัพธ์ที่สนใจ คือ หน้าของแต่ละเหรียญ จงหาปริภูมิตัวอย่าง และเหตุการณ์ที่เหรียญออกหัวอย่างน้อย 1 ครั้ง
วิธีทำ
- ให้ H แทนเหรียญออกหัว
- T แทนเหรียญออกก้อย
- E คือ เหตุการณ์ที่ออกหัวอย่างน้อย 1 ครั้ง
ดังนั้น
- S = {HH, HT, TH, TT}
- E = {HH, HT, TH}
ตัวอย่าง ในกล่องใบหนึ่งมีสลากหมายเลข 1 ถึง 9 อยู่หมายเลขละ 1 ใบ สุ่มหยิบสลากขึ้นมา 2 ใบ พร้อมๆกัน จงหาเหตุการณ์ที่ผลรวมของหมายเลขที่หยิบได้เป็น 9
วิธีทำ
- S = เหตุการณ์ทั้งหมดที่เป็นไปได้ในการหยิบสลาก 2 ใบขึ้นมาพร้อมกัน
- S = {(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8), (1,9), (2,3), (2,4), (2,5), (2,6), (2,7), (2,8), (2,9), (3,4), (3,5), (3,6), (3,7), (3,8), (3,9), (4,5), (4,6), (4,7), (4,8), (4,9), (5,6), (5,7), (5,8), (5,9), (6,7), (6,8), (6,9), (7,8), (7,9), (8,9)}
- E คือ เหตุการณ์ที่ผลลัพธ์รวมกันได้ 9
ดังนั้น
- E = {(1,8), (2,7), (3,6), (4,5)}
ความน่าจะเป็น
ต่อเนื่องจากการทดลองสุ่มและเหตุการณ์ ให้ S เป็นปริภูมิตัวอย่างที่เป็นเซตจำกัด และสมาชิกทุกตัวของ S มีโอกาสเกิดขึ้นเท่าๆกัน และ E เป็นเหตุการณ์ที่เป็นสับเซตของ S
ความน่าจะเป็นของเหตุการณ์ E เขียนแทนด้วย P(E) โดย
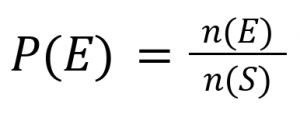
สมบัติของความน่าจะเป็น
- 0 ≤ P(A) ≤ 1 หรือ ความน่าจะเป็นจะมีค่าระหว่าง 0 ถึง 1
- P(S) = 1
- P(∅) = 0
- P(A∪B) = P(A) + P(B) – P(A∩B)
- P(A’) = 1 – P(A)
- P(A-B) = P(A) – P(A∩B)
- ให้ H แทนเหรียญออกหัว
- T แทนเหรียญออกก้อย
- E คือ เหตุการณ์ที่ออกหัวอย่างน้อย 1 ครั้ง
- S = {HH, HT, TH, TT}
- E = {HH, HT, TH}
- P(E) = n(E)⁄n(S) = 3⁄4
- S = เหตุการณ์ทั้งหมดที่เป็นไปได้ในการหยิบสลาก 2 ใบขึ้นมาพร้อมกัน
- S = {(1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (1,8), (1,9), (2,3), (2,4), (2,5), (2,6), (2,7), (2,8), (2,9), (3,4), (3,5), (3,6), (3,7), (3,8), (3,9), (4,5), (4,6), (4,7), (4,8), (4,9), (5,6), (5,7), (5,8), (5,9), (6,7), (6,8), (6,9), (7,8), (7,9), (8,9)}
- E คือ เหตุการณ์ที่ผลลัพธ์รวมกันได้ 9
- E = {(1,8), (2,7), (3,6), (4,5)}
- P(E) = n(E)⁄n(S) = 4⁄36
คุยกันท้ายบท
1. นักเรียนห้องหนึ่งมีจำนวน 30 คน สอบวิชาคณิตศาสตร์ได้เกรด A 5 คน ได้เกรด B 15 คน และได้เกรด C 10 คน ถ้าสุ่มนักเรียน 3 คน จากห้องนี้ แล้วความน่าจะเป็นที่จะได้นักเรียนอย่างน้อย 1 คน ที่ได้เกรด A เท่ากับเท่าใด (สามัญ ปี’56)
เฉลย
2. กิตติและสมาน กับเพื่อนๆรวม 7 คน ไปเที่ยวต่างจังหวัดด้วยกัน ในการค้างแรมที่มีบ้านพัก 3 หลัง หลังแรกพักได้ 3 คน ส่วนหลังที่สองและสามพักได้หลังละ 2 คน ซึ่งแต่ละหลังมีความแตกต่างกัน พวกเขาจึงตกลงที่จะจับสลากว่าใครจะได้พักบ้านหลังใด ความน่าจะเป็นที่กิตติและสมานจะได้พักบ้านหลังเดียวกันในหลังที่หนึ่งหรือหลังที่สามเท่ากับเท่าใด (PAT1 มี.ค. ปี’52)
เฉลย
เป็นยังไงกันบ้างครับกับเนื้อหาและแบบฝึกหัดของ “ความน่าจะเป็น” ไม่ยากเกินไปใช่ไหมครับ น้องๆจะเห็นได้ว่าเนื้อหาของบทนี้ค่อนข้างสั้น แต่มีการนำเรื่องของการเรียงสับเปลี่ยนและการจัดหมู่จากเนื้อหา “หลักการนับเบื้องต้น” มาใช้ในบทนี้ด้วย และเนื้อหาของเรื่อง “ความน่าจะเป็น” นั้นจะเป็นพื้นฐานไปสู่เรื่องของ “สถิติ” ในตอนเรียนชั้น ม.6 อีกด้วย รวมไปถึงน้องๆคนไหนที่กำลังสนใจเรียนต่อระดับมหาวิทยาลัยในสาขาที่เกี่ยวข้องกับคณิตศาสตร์เช่น สาขาสถิติประยุกต์ สาขาคณิตศาสตร์ประยุกต์ สาขาวิทยาการคอมพิวเตอร์ ต่างก็ใช้ความรู้ และความเข้าใจในพื้นฐานของความน่าจะเป็นกันทั้งหมด ดังนั้นแล้วน้องๆทุกคนควรจะเตรียมตัว และทำความเข้าใจเนื้อหาโดยละเอียด
และจากบทความที่แล้วพี่นอตได้เกรินเอาไว้แล้วว่า จากสถิติที่ผ่านเนื้อหาในส่วนของความน่าจะเป็น และหลักการนับเบื้องต้นมักจะถูกรวมกันนำไปออกข้อสอบ A – Level ประมาณ 3-4 ข้ออยู่เป็นประจำ ดังนั้นถ้าน้องๆได้ลองทำแบบฝึกหัดท้ายบทที่พี่นอตได้แนบไว้ น้องๆน่าจะเก็บคะแนนจากส่วนนี้ได้ไม่ยากอย่างแน่นอน แต่ถ้าน้องๆคนไหนอยากได้เนื้อหาที่ละเอียดมากกว่านี้ รวมไปถึงแบบฝึกหัดที่เข้มข้นกว่านี้ พี่นอตขอแนะนำคอร์สวิชา “คณิตศาสตร์ ม.5 เทอม 2” จาก Panya Society ที่มีการปูพื้นฐานตั้งแต่ง่ายไปจนถึงระดับยาก เน้นความเข้าใจ ไม่เน้นกาารท่องจำ พร้อมทั้งแบบฝึกหัด รวมไปถึงตัวอย่างข้อสอบจากข้อสอบจริงในการสอบเข้าระดับมหาวิทยาลัย A – Level
สุดท้ายนี้พี่นอตหวังว่า น้องๆจะสนุกกับการเรียนคณิตศาสตร์ ม.5 เทอม 2 ไปตลอดทั้งเทอม และขอให้น้องๆประสบความสำเร็จในการเรียนเทอมนี้ ได้เกรดดังหวัง คะแนนปังกันทุกคนเลยนะครับ แล้วพบกันในบทความชุดถัดไปนะครับ รับรองว่าติดตาม Panya Society กันไว้ไม่ผิดหวังแน่นอน 🙂
คณิตศาสตร์ ม.5 เทอม 2
- อดีต Senior Software Engineer ที่ Google กว่า 10 ปี
- ได้รับทุนเล่าเรียนหลวงไปศึกษาระดับปริญญาตรี ด้าน Electrical and Computer Engineering และ Computer Science ที่ Carnegie Mellon University สหรัฐอเมริกา
- จบปริญญาเอก ด้าน Artificial Intelligence พร้อมรางวัลนักเรียนดีเด่นจาก UCLA
- ผลงานวิจัยด้าน Artificial Intelligence (AI) ของพี่นอตได้รับรางวัลงานวิจัยดีเยี่ยมจาก สำนักงานคณะกรรมการวิจัยแห่งชาติในปี 2557
ทำความรู้จัก พี่นอต (ดร.ธรรมนิติ์ พิพัฒน์ศรีสวัสดิ์)
Math Magic


















