สรุปเนื้อหาที่สำคัญ
“เซต” คือบทแรกของคณิตศาสตร์ ม. 4 เทอม 1 และยังเป็นบทเรียนแรกสุดของวิชาคณิตศาสตร์ ในระดับชั้นมัธยมปลายอีกด้วย และก็ยังเป็นบทสำคัญในการนำไปใช้เป็นพื้นฐานเพื่อประยุกต์สู่เนื้อหาวิชาคณิตศาสตร์ระดับชั้นมัธยมปลายที่จะมีความเข้มข้นขึ้น เช่น “ความสัมพันธ์และฟังก์ชัน” “หลักการนับเบื้องต้น” เป็นต้น
นั้นทำให้บทเรียนคณิตศาสตร์ ม.4 เทอม 1 เรื่อง “เซต” มีความสำคัญอย่างยิ่งที่น้องๆจะต้องทำความเข้าใจเนื้อหาโดยละเอียด และปูพื้นฐานของบทนี้ให้แน่น เพื่อพร้อมรับมือกับการเรียนวิชาคณิตศาสตร์ ม.ปลาย และใช้ในการทำข้อสอบที่มีความหลากหลายและโจทย์ที่ประยุกต์หลายๆ บทเรียนเข้าไว้ด้วยกัน เพื่อวัดความรู้ความเข้าใจ โดยมี “เซต” เป็นส่วนหนึ่งของชุดความรู้สำคัญที่จำเป็นต้องนำไปประยุกต์ได้ในข้อสอบเข้ามหาวิทยาลัย TCAS ต่อไป ในข้อสอบ A – Level ดังนั้นน้องๆ อย่าทิ้งบทนี้นะครับ หมั่นทบทวนเนื้อหา และไม่ลืมที่จะเก็บเนื้อหาสาระสำคัญต่างๆด้วยนะครับ
เนื้อหาหลักของบทนี้ประกอบด้วย รายละเอียดบทย่อย ดังนี้
ความรู้เบื้องต้นเกี่ยวกับเซต
นิยามของเซต เซต คือ คำที่ใช้บ่งบอกกลุ่มของสิ่งต่าง ๆ ทำให้ทราบว่าเมื่อพูดถึงกลุ่มใดแล้วก็จะทราบได้อย่างแน่นอนว่าสิ่งใดอยู่ในกลุ่ม และสิ่งใดไม่อยู่ในกลุ่ม โดยจะเรียกสิ่งที่อยู่ในเซตว่า สมาชิกของเซต เช่น
เซตของอักษรสระในภาษาอังกฤษ หมายถึง กลุ่มของอักษร a, e, i, o, และ u- จำนวนสมาชิกเซต A เขียนแทนด้วย n(A)
- a เป็นสมาชิกของเซต A เขียนแทนด้วย a ∈ A
- b ไม่เป็นสมาชิกของเซต A เขียนแทนด้วย b ∉ A
การเขียนเซต เซตสามารถเขียนได้สองแบบคือ แบบแจกแจงสมาชิก กับ แบบมีเงื่อนไข
- แบบแจกแจงสมาชิก แสดงสมาชิกทุกตัวที่อยู่ในเซตนั้นในวงเล็บ { } คั่นด้วยเครื่องหมาย , เช่น A = { a, b, c, d, f }
- แบบบอกเงื่อนไข แสดงสมาชิกโดยการเขียนเป็นเงื่อนใข ในรูป {สมาชิก I เงื่อนไข} เช่น B = { 2, 4, 6, 8 | จำนวนเต็มคู่บวกที่น้อยกว่า 10 }
ชนิดของเซต
- เซตอนันต์ มีจำนวนสมาชิกมากไม่มีสิ้นสุด เช่น เซตของจำนวนเต็มบวก = { 1, 2, 3, 4, … }
- เซตจำกัด สามารถบอกจำนวนสมาชิกได้ เช่น เซตของชื่อวันในสัปดาห์ = { วันจันทร์, วันอังคาร, วันพุธ, … , วันเสาร์, วันอาทิตย์ }
- เซตว่าง (∅, { }) เป็นเซตที่ไม่มีสมาชิกเลย และเซตว่างก็นับว่าเป็นเซตจำกัด
การเท่ากันของเซต การเท่ากันของเซต จะต้องมีจำนวนสมาชิกเท่ากัน และสมาชิกเหมือนกันทุกตัว (สลับที่สมาชิกได้) สมาชิกที่ซ้ำกันจะนับเป็นตัวเดียวกันไม่นับซ้ำ เขียนแทนด้วย A = B
เอกภพสัมพัทธ์ คือ ขอบเขตที่เราสนใจ สมาชิกทุกตัวของเซตต่าง ๆ จะต้องอยู่ในเอกภพสัมพัทธ์ มักใช้สัญลักษณ์ U
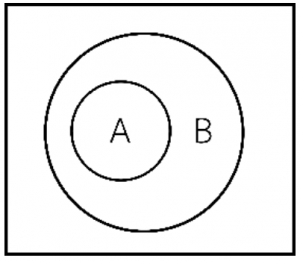
สับเซต A เป็นสับเซตของ B แปลว่าสมาชิกทุกตัวของ A ต้องมีอยู่ใน B จะเป็นเซตที่เท่ากันเลยก็ได้ (เซตว่างเป็นสับเซตของทุกเซต มีสัญลักษณ์การเป็น และไม่เป็นสับเซต คือ ⊂, ⊄ ตามลำดับ) เช่น กำหนดให้
- A = { 1, 2, 3, 4, 5 }
- B = { 2, 4 }
- C = { 3, 5, 7 }
ดังนั้น B ⊂ A แต่ C ⊄ A
สมบัติเกี่ยวกับสับเซตที่น่าสนใจ
- ถ้า A ⊂ B และ B ⊂ A แล้ว A = B
- ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C
- เซตทุกเซตเป็นสับเซตของตัวเอง คือ ถ้า A เป็นเซตใดๆ แล้ว A ⊂ A
- เซตว่างเป็นสับเซตของทุกเซต คือ ถ้า A เป็นเซตใดๆ แล้ว ∅ ⊂ A
- ถ้า n(A) = n แล้ว จำนวนสับเซตของเซต A เท่ากับ 2n สับเซต
พาวเวอร์เซต พาวเวอร์เซตของ A เขียนแทนด้วย P(A) หมายถึง เซตของสับเซตทั้งหมดของ A และจำนวนของสมาชิกของพาวเวอร์เซตหาได้จาก
n(P(A))= 2n
เช่น กำหนดให้ A = { 1, 2 } จงหาสับเซต และพาวเวอร์เซตของ Aวิธีทำ
- สับเซตทั้งหมดของ A คือ ∅, {1}, {2}, {1,2}
- ดังนั้น พาวเวอร์เซตของ P(A) = { ∅, {1}, {2}, {1,2} }
- n(P(A))= 2n = 22 = 4
สมบัติเกี่ยวกับพาวเวอร์เซตที่น่าสนใจ เมื่อ A, B, X เป็นเซตใดๆ
- X ∈ P(A) ก็ต่อเมื่อ X ⊂ A
- A ∈ P(A)
- สำหรับทุกเซต A ใดๆ จะได้ว่า ∅ ∈ P(A) และ ∅ ⊂ P(A) ด้วย
- P(A) ≠ ∅ สำหรับทุกๆเซต A
- P(∅) = {∅}
- A ⊂ B ก็ต่อเมื่อ P(A) ⊂ P(B)
- ถ้า A เป็นเซตจำกัด ซึ่ง n(A) = n แล้ว n(P(A)) = 2n
- ถ้า A เป็นเซตอนันต์ แล้ว P(A) เป็นเซตอนันต์
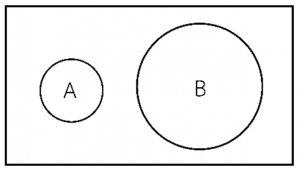
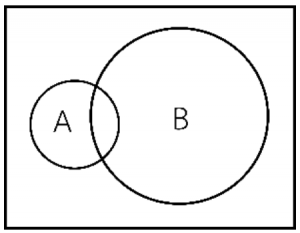
แผนภาพเวนน์ออยเลอร์
การดำเนินการระหว่างเซต
- ยูเนียน (∪) A ∪ B คือ เซตของสมาชิกทั้งหมดของ A รวมกับสมาชิกทั้งหมดของ B โดยตัวซ้ำนับเป็นตัวเดียว
- อินเตอร์เซกชัน (∩) A ∩ B คือ เซตของสมาชิกทั้งหมดของ A และ B ที่ซ้ำกัน
- ผลต่างระหว่างเซต (-) A – B คือ เซตของสมาชิกทั้งหมดของ A แต่ไม่เป็นสมาชิกของ B
- คอมพลีเมนต์ (‘) A’ คือ เซตของสมาชิกทั้งหมดของเอกภพสัมพัทธ์ แต่ไม่เป็นสมาชิกของเซต A
ตัวอย่าง กำหนดให้
- U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
- A = {2, 4, 6, 8}
- B = {2, 3, 5, 7}
ดังนั้น
- A ∪ B = {2, 3, 4, 5, 6, 7, 8}
- A ∩ B = {2}
- A – B = {4, 6, 8}
- B – A = {3, 5, 7}
- A’ = {1, 3, 5, 7, 9}
- B’ = {1, 4, 6, 8, 9}
คุณสมบัติของการดำเนินการระหว่างเซต
- (A ∪ B)’ = A’ ∩ B’
- (A ∩ B)’ = A’ ∪ B’
- (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C)
- (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)
การแก้ปัญหาโดยใช้เซต
- n(B – A) = n(B) – n(A ∩ B)
- n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
- n(A ∪ B ∪ C) = n(A) + n(B) + n(C) – n(A ∩ B) – n(A ∩ C) – n(B ∩ C) + n(A ∩ B ∩ C)
ตัวอย่าง นักเรียนชั้น ม.4 ในโรงเรียนแห่งหนึ่งมีจำนวน 100 คนได้รับรางวัลเรียนดี 30 คน ได้รับรางวัลมารยาทดี 50 คน ในจำนวนนี้ได้รับรางวัลทั้งสองประเภท 20 คน จงหา
- จำนวนนักเรียนทั้งหมดที่ได้รับรางวัล
- จำนวนนักเรียนที่ไม่ได้รับรางวัลใดๆเลย
วีธีทำ
- ให้ A แทนเซตนักเรียนที่ได้รับรางวัลเรียนดี
- ให้ B แทนเซตนักเรียนที่ได้รับรางวัลมารยาทดี
จากโจทย์จะได้ n(U) = 100, n(A) = 30, n(B) = 50, n(A ⋂ B) = 20
- จำนวนนักเรียนทั้งหมดที่ได้รับรางวัล เขียนแทนด้วย n(A ⋃ B)
- จาก n(A ⋃ B) = n(A) + n(B) – n(A ⋂ B)
- จะได้ n(A ⋃ B) = 30 + 50 – 20 = 60
- ดังนั้น จำนวนนักเรียนทั้งหมดที่ได้รับรางวัล คือ 60 คน
- จำนวนนักเรียนที่ไม่ได้รับรางวัลใดๆเลย เขียนแทนด้วย n((A ⋃ B)’)
- จาก n((A ⋃ B)’) = n(U) – n(A ⋃ B)
- จะได้ n((A ⋃ B)’) = 100 – 60 = 40
- ดังนั้น จำนวนนักเรียนที่ไม่ได้รับรางวัลใดๆเลย คือ 40 คน
คุยกันท้ายบท
- ในการสำรวจความเห็นของนักเรียนชั้นมัธยมศึกษาตอนปลายจำนวน 880 คน เพื่อสอบถามข้อมูลเกี่ยวกับ
การศึกษาต่อ ปรากฏผลดังนี้
มีผู้ต้องการศึกษาต่อ 725 คน
มีผู้ต้องการทำงาน 160 คน
มีผู้ต้องการศึกษาต่อหรือทำงาน 813 คน
ผู้ต้องการศึกษาต่อและทำงานด้วยมีจำนวนเท่ากับเท่าใด?
เฉลย - กำหนดให้ A, B และ C เป็นเซตใดๆ ถ้า
n( A ∪ B ∪ C ) = 91,
n( A ∩ B′ ∩ C′ ) = 11,
n(( B – A ) ∩ ( B – C )) = 15,
n( A ∩ B ∩ C ) = 20,
n(( A ∩ B ) ∪ ( A ∩ C ) ∪ ( B ∩ C )) = 47 และ
n( C ) = 59
แล้ว n( A′ ∩ B′ ∩ C ) เท่ากับเท่าใด?
เฉลย
เป็นยังไงกันบ้างครับกับเนื้อหาและแบบฝึกหัดของเรื่อง “เซต” คงจะไม่ยากเกินไปใช่ไหมครับ รวมไปถึงตอนนี้น้องๆคงจะเห็นได้ว่าวิชาคณิตศาสตร์ ม.ปลาย มีความแตกต่างกันอย่างไรกับตอนช่วง ม.ต้น ซึ่งวิชาคณิตศาสตร์ ม.4 เทอม 1 จะเป็นช่วงของการปูพื้นฐาน และปรับความพร้อมให้กับน้องๆในการเรียนวิชาคณิตศาสตร์ ม.ปลาย ไปทั้งตลอดระดับชั้น และอย่างที่พี่นอตได้เกรินไว้ว่าเรื่อง “เซต” นี้เองก็จะเป็นพื้นฐานในการต่อยอดไปยังเนื้อหาอื่นๆ เช่น “ความสัมพันธ์และฟังก์ชัน” “หลักการนับเบื้องต้น” ซึ่งจะมีความซับซ้อนเพิ่มขึ้นไปอีก ดั้งนั้นพี่จึงอยากให้น้องๆทุกคนควรให้ความสำคัญกับการเรียนเพื่อความเข้าใจสูงสุดในเนื้อหาของบทเรียนต่างๆ พร้อมกับฝึกทำโจทย์บ่อยๆ
และถ้าน้องๆคนไหนอยากได้เนื้อหาที่ละเอียดกว่านี้ รวมไปถึงแบบฝึกหัดที่เข้มข้นกว่านี้ พี่นอตขอแนะนำคอร์สวิชา “คณิตศาสตร์ ม.4 เทอม 1” จากทาง Panya Society ที่มีการปูพื้นฐานตั้งแต่ง่ายไปจนถึงระดับยาก เน้นความเข้าใจ ไม่เน้นการท่องจำ พร้อมทั้งแบบฝึกหัด รวมไปถึงตัวอย่างข้อสอบจากข้อสอบจริงในการสอบเข้าระดับมหาวิทยาลัย A – Level ทำให้คอร์สนี้เหมาะกับน้องๆ ทุกคนที่อยู่ชั้น ม.4 ที่โรงเรียนใช้หลักสูตรใหม่ (2560) ที่เบื่อกับการเรียนคณิตฯแบบท่องจำ แต่ดันทำโจทย์ไม่ได้ หรือไปเรียนพิเศษคณิตศาสตร์จากที่อื่นมาแล้วก็ยังไม่เข้าใจ ด้วยการสอนคณิตศาสตร์อย่างบูรณาการในคอร์สนี้ พี่ๆทั้งสองคนรับรองได้เลยว่าคอร์สจากทาง Panya Society นี้จะแตกต่างกับที่เรียนพิเศษคณิตศาสตร์ที่อื่นๆ อย่างแน่นอน
สุดท้ายนี้พี่หวังว่า น้องๆจะสนุกกับการเรียนคณิตศาสตร์ ม.4 เทอม 1 รวมไปถึงวิชาคณิตศาสตร์ ม.ปลายไปตลอดทั้งระดับชั้น และขอให้น้องๆประสบความสำเร็จในการเรียนเทอมนี้ ได้เกรดดังหวัง คะแนนปังทุกคนเลยครับ แล้วกันใหม่ในสรุปเนื้อหาเรื่อง “ตรรกศาสตร์” นะครับ 🙂
- อดีต Senior Software Engineer ที่ Google กว่า 10 ปี
- ได้รับทุนเล่าเรียนหลวงไปศึกษาระดับปริญญาตรี ด้าน Electrical and Computer Engineering และ Computer Science ที่ Carnegie Mellon University สหรัฐอเมริกา
- จบปริญญาเอก ด้าน Artificial Intelligence พร้อมรางวัลนักเรียนดีเด่นจาก UCLA
- ผลงานวิจัยด้าน Artificial Intelligence (AI) ของพี่นอตได้รับรางวัลงานวิจัยดีเยี่ยมจาก สำนักงานคณะกรรมการวิจัยแห่งชาติในปี 2557
ตัวอย่างการสอน โดยพี่นอต
Math Magic

เรียนสนุก ทำโจทย์คล่อง สอบให้ติด
: คอร์สแนะนำ :
TAG:
คณิตศาสตร์, ม.4, เทอม 1, เซต, PAT1, 9 วิชาสามัญ, A – Level