สรุปเนื้อหาที่สำคัญ
“ความสัมพันธ์ และฟังก์ชัน” คือบทแรกของคณิตศาสตร์ ม. 4 เทอม 2 เป็นบทสำคัญที่จำเป็นจะต้องนำไปใช้เป็นพื้นฐานเพื่อประยุกต์สู่เนื้อหาในบทต่อไปที่จะมีความเข้มข้นขึ้น กล่าวคือใช้ในเรื่อง “ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม”
นับว่าบทเรียนคณิตศาสตร์ ม.4 เทอม 2 เรื่องความสัมพันธ์ และฟังก์ชัน มีความสำคัญอย่างยิ่งที่น้องๆจะต้องทำความเข้าใจเนื้อหาโดยละเอียด และอัดพื้นฐานของบทนี้ให้แน่น เพื่อพร้อมรับมือกับการทำข้อสอบที่มีความหลากหลาย และโจทย์ที่ประยุกต์หลายบทเข้าไว้ด้วยกัน เพื่อวัดความรู้ความเข้าใจ โดยมีความสัมพันธ์ และฟังก์ชัน เป็นส่วนหนึ่งของชุดความรู้สำคัญที่จำเป็นต้องนำไปประยุกต์ได้ในข้อสอบเข้ามหาวิทยาลัย TCAS ในข้อสอบ A – Level น้องๆอย่าทิ้งบทนี้ หมั่นทบทวนเนื้อหา และไม่ลืมที่จะเก็บเนื้อหาสาระสำคัญต่างๆด้วยนะครับ
ความสัมพันธ์และฟังก์ชัน มีหน่วยย่อย ดังนี้
- คู่อันดับและผลคูณคาร์ทีเซียน
- ความสัมพันธ์
- กราฟของความสัมพันธ์
- การประยุกต์ของกราฟ
- ฟังก์ชัน
- ฟังก์ชันต่างๆ บางชนิด
- แบบต่างๆ ของฟังก์ชัน
- ฟังก์ชันผกผัน
- การบวก การลบ การคูณ การหาร และการคูณด้วยจำนวนจริงของฟังก์ชัน
- ฟังก์ชันประกอบ
ความสัมพันธ์
ความสัมพันธ์ในทางคณิตศาสตร์นั้น มีความคล้ายกับความสัมพันธ์ในชีวิตจริงที่เราคุ้นเคย คือเป็นการแสดงความเกี่ยวข้องกันของสองสิ่ง ซึ่งในทางคณิศาสตร์เรียกว่า คู่อันดับ ซึ่งมีนิยามดังนี้
คู่อันดับ คือ การนำสิ่ง สองสิ่ง มาเขียนคู่กัน โดยคำนึงถึงลำดับด้วย ซึ่งเขียนได้ดังนี้
คู่อันดับ a, b เขียนแทนด้วย (a, b) โดยเรียก a ว่า สมาชิกตัวหน้าของคู่อันดับ และเรียก b ว่า สมาชิกตัวหลังของคู่อันดับ เช่น
- (โตเกียว, ญี่ปุ่น)
- (มกราคม, 31)
- (แบงค์, จอย)
- (99, 38)
- (-9, 36.9)
การเท่ากันของคู่อันดับ หมายถึง (x1, y1) = (x2, y2)
ก็ต่อเมื่อ x1 = y1 และ x2 = y2 หรือก็คือ ตัวหน้า = ตัวหน้า, ตัวหลัง = ตัวหลัง
เมื่อรู้จักคู่อันดับแล้ว ความสัมพันธ์ มีนิยามดังต่อไปนี้
ความสัมพันธ์ คือ เซตที่มีสมาชิกทุกตัวเป็นคู่อันดับ โดยที่คู่อันดับแต่ละคู่ เกิดจากการจับคู่กันของสมาชิกจากเซตสองเซต เช่น
- {(A, X), (B, Y), (C, Z), (D, W)}
- {(Galaxy Note 10, Samsung), (iPhone 11, Apple), (Find X, Oppo), …}
- {(1, 1), (2, 4), (3, 9), …}
ตัวอย่างโจทย์ – จงหาค่า x,y เมื่อ (x + 1, 2y) = (-5, 11) เฉลย
ผลคูณคาร์ทีเชียน เป็นการกระทำกันระหว่างเซต 2 เซต โดยผลคูณคาร์ทีเชียนระหว่างเซต A และ B เขียนแทนด้วย A×B คือ เซตของคู่อันดับ (a,b) ทั้งหมด โดยที่ a เป็นสมาชิกของเซต A และ b เป็นสมาชิกของเซต B เขียนอยู่ในรูปแบบดังนี้
A×B = {(a,b) | a ∈ A และ b ∈ B}
***ข้อสังเกต “ความสัมพันธ์ระหว่างเซต A,B ทุกอันต้องเป็นสับเซตของ A×B”***
ตัวอย่างโจทย์ – จงหาผลคูณคาร์ทีระหว่างเซตต่อไปนี้ {a, b} และ {a, b, c} เฉลย
สมบัติของผลคูณคาร์ทีเชียน ให้ A, B และ C เป็นเซตใด ๆ และ n(A) คือ จำนวนสมาชิกของเซต A
- A×{} = {}
- {}×A = {}
- A×(B∪C) = (A×B)∪(A×C)
- A×(B∩C) = (A×B)∩(A×C)
- A×(B-C) = (A×B) – (A×C)
- n(A×B) = n(A).n(B)
ความสัมพันธ์จาก A ไป B ให้ A และ B เป็นเซตใด ๆ แล้ว r เป็นความสัมพันธ์จาก A ไป B ก็ต่อเมื่อ r เป็นสับเซตของ AB เขียนได้ว่า
r = {(a,b) | (a,b) ∈ A×B}
ความสัมพันธ์แบบมีเงื่อนไข คือ เซตของคู่อันดับ โดยที่สมาชิกตัวหน้าของแต่ละคู่อันดับ สัมพันธ์กับสมาชิกตัวหลัง ในรูปแบบเดียวกันในทุก ๆ คู่อันดับ เช่น
- A = {โตเกียว, กรุงเทพ, จาการ์ต้า, ปักกิ่ง, โซล}
- B = {ไทย, จีน, ญี่ปุ่น, เกาหลี, อินโดนีเซีย, อินเดีย, รัสเซีย}
ความสัมพันธ์จาก A ไป B แบบ “เมืองหลวง – ประเทศ” คือ {(โตเกียว, ญี่ปุ่น), (กรุงเทพ, ไทย), (จาการ์ต้า, อินโดนีเซีย), (ปักกิ่ง, จีน), (โซล, เกาหลี)}
หรือเขียนแบบบอกเงื่อนไขได้ว่า {(a, b) ∈ A×B | a เป็นเมืองหลวงของ b}
- A = {1, 3, 5, 7, 9}
ความสัมพันธ์จาก A ไป A แบบ “บวกกันได้ 10” คือ {(1, 9), (3, 7), (5, 5), (7, 3), (9, 1)}
หรือเขียนแบบบอกเงื่อนไขได้ว่า {(a, b) ∈ A×A | a + b = 10}
กราฟของความสัมพันธ์ หากความสัมพันธ์ เป็นความสัมพันธ์ระหว่างตัวเลขแล้ว เราสามารถเขียนความสัมพันธ์โดยใช้กราฟได้ โดยการนำคู่อันดับต่างๆ ของความสัมพันธ์ไปวาดลงบนกราฟ เช่น
ให้ A = {0, 1, 2, 3, 4, 5}
B = {5, 6, 7, …, 20}
โดย r = {(x, y) ∈ A×B | y = 3x}
แจกแจงสมาชิกได้เป็น r = {(2, 6), (3, 9), (4, 12), (5, 15)}
จะวาดกราฟได้ดังนี้
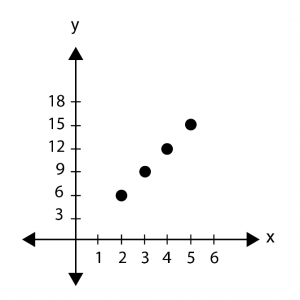
ในกรณี r เป็นความสัมพันธ์ของจำนวนจริง มักจะวาดกราฟได้เป็นเส้น เช่น
r = {(x, y) ∈ R×R | y = 3x}
จะวาดกราฟได้ดังนี้
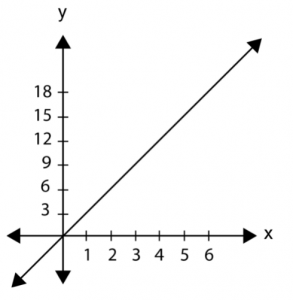
เคล็ดลับการพิจารณากราฟ พิจารณากราฟของความสัมพันธ์ระหว่าง x และ y ได้ดังนี้
- กราฟจะผ่านจุด (a, b) เมื่อ แทนค่า a และ b ลงในสมการแล้วทำให้สมการเป็นจริง
- จุดตัดแกน x คือ จุดที่ y = 0 ถ้าแทนค่าแล้วสมการไม่เป็นจริงแสดงว่า ไม่มีจุดตัดแกน x
- จุดตัดแกน y คือ จุดที่ x = 0 ถ้าแทนค่าแล้วสมการไม่เป็นจริงแสดงว่า ไม่มีจุดตัดแกน y
- กราฟอยู่เหนือแกน x เมื่อ y > 0
- กราฟอยู่ใต้แกน x เมื่อ y < 0
ตัวอย่างโจทย์ – กราฟต่อไปนี้ผ่านจุด (0, 1) หรือไม่
ตัวอย่างโจทย์ – จงหาจุดตัดแกน x และ y ของกราฟต่อไปนี้
- 2x + 1 = 3y เฉลย
โดเมนและเรนจ์ของความสัมพันธ์
โดเมนของความสัมพันธ์ r คือ เซตของ สมาชิกตัวหน้าของคู่อันดับทุกคู่ ในความสัมพันธ์ r โดเมนของความสัมพันธ์ r เขียนแทนด้วย Dr
Dr = {x | (x, y) ∈ r}
เรนจ์ของความสัมพันธ์ r คือ เซตของ สมาชิกตัวหลังของคู่อันดับทุกคู่ ในความสัมพันธ์ r เรนจ์ของความสัมพันธ์ r เขียนแทนด้วย Rr
Rr = {y | (x, y) ∈ r}
เช่น
r = {(1, 3), (2, 8), (3, 10), (3, -5), (4, 19), (8, 3), (100, -5), (-9, 22)}
Dr = {1, 2, 3, 4, 8, 100, -9}
Rr = {3, 8, 10, -5, 19, -5, 22}
r = {(โตเกียว, ญี่ปุ่น), (กรุงเทพ, ไทย), (เบอร์ลิน, เยอรมันนี), (แคนเบอร์ร่า, ออสเตรเลีย), (โซล, เกาหลี), …}
Dr = เซตของเมืองหลวงทั่วโลก
Rr = เซตของประเทศทุกประเทศ
ฟังก์ชัน
ฟังก์ชัน คือ ความสัมพันธ์รูปแบบหนึ่งที่สมาชิกในโดเมนแต่ละตัวจับคู่กับ สมาชิกในเรนจ์ของความสัมพันธ์ เพียงตัวเดียวเท่านั้น เช่น
{(1,a), (2,b), (3,c), (4,d)} เป็นฟังก์ชัน
{(1,a), (2,a), (3,a), (4,a)} เป็นฟังก์ชัน
{(1,a), (1,b), (3,c), (4,d)} ไม่เป็นฟังก์ชัน เพราะมี 1 ที่จับคู่กับทั้ง aและb
ข้อสังเกตฟังก์ชันอย่างเร็วๆ
- ถ้าสมาชิกตัวหน้าของแต่ละคู่อันดับไม่ซ้ำกัน จะเป็นฟังก์ชัน
- ถ้ามีสมาชิกตัวหน้าคู่อันดับซ้ำกัน อย่างน้อย 1 คู่อันดับ จะไม่เป็นฟังก์ชัน
- ความสัมพันธ์ที่มี y ยกกำลังเป็นเลขคู่ หรือ y อยู่ในเครื่องหมายค่าสัมบูรณ์ จะไม่เป็นฟังก์ชัน
การนิยามฟังก์ชัน ถ้า f เป็นฟังก์ชัน และ (x, y) ∈ f จะได้ว่า y เป็นค่าของฟังก์ชัน f ที่ x เขียนแทนด้วย f(x) หรือ y = f(x) เรียก f(x) = (ค่าในเทอมของ x) ว่า นิยามของฟังก์ชัน ดังเช่น
ถ้า f เป็นฟังก์ชันของ x แล้ว เราสามารถหาค่า f(k) ได้โดย
สมมุติให้ x = k แล้วหาค่า f(x) เมื่อแทน x = k
นิยามของฟังก์ชัน คือ f(x) = x2 + 1
f(5) คือ สมมุติ x = 5 หาค่า x2 + 1
จะได้ว่า f(5) = 52 + 1 = 26
f(-1) คือ สมมุติ x = -1 หาค่า x2 + 1
จะได้ว่า f(-1) = (-1)2 + 1 = 2
f(a + b) คือ สมมุติ x = a + b หาค่า x2 + 1
จะได้ว่า f(a+b) = (a+b)2 + 1 = a2 + 2ab + b2 + 1
รูปแบบต่างๆของฟังก์ชัน มีดังต่อไปนี้
ฟังก์ชันจาก A ไป B
f เป็นฟังก์ชันจาก A ไป B เขียนแทนด้วย f:A→B
หมายความว่า ทุกสมาชิกใน A ต้องมีคู่กับสมาชิกใน B
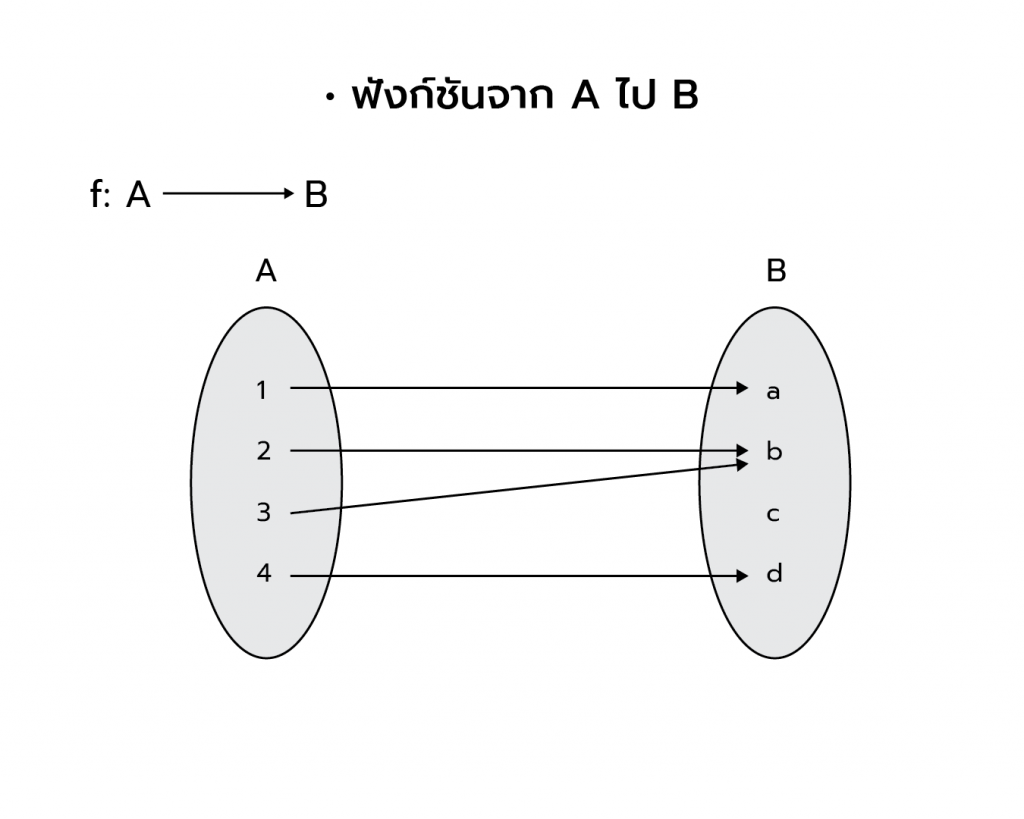
ฟังก์ชันจาก A ไปทั่วถึง B
f เป็นฟังก์ชันจาก A ไปทั่วถึง B เขียนแทนด้วย f:A onto→ B
หมายความว่า ทุกสมาชิกใน A และ B ต้องมีคู่
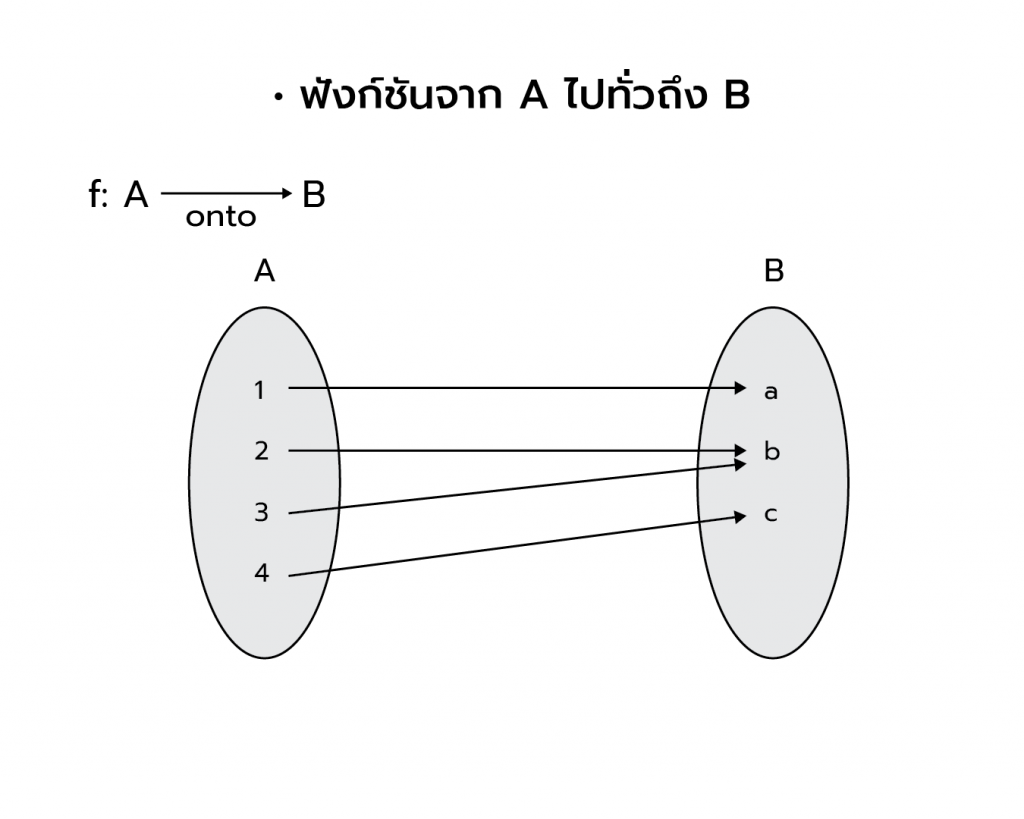
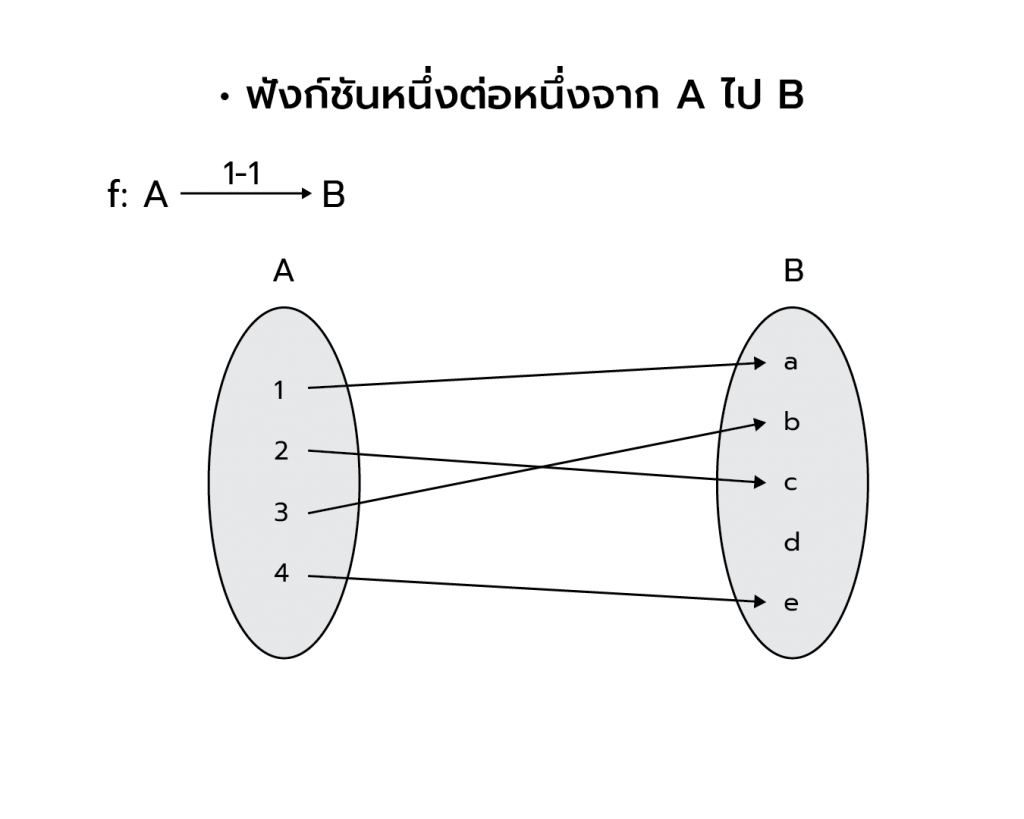
ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B
f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B เขียนแทนด้วย f:A 1-1→ B
หมายความว่า ทุกสมาชิกใน A ต้องมีคู่กับสมาชิกใน B และคู่ไม่ซ้ำ
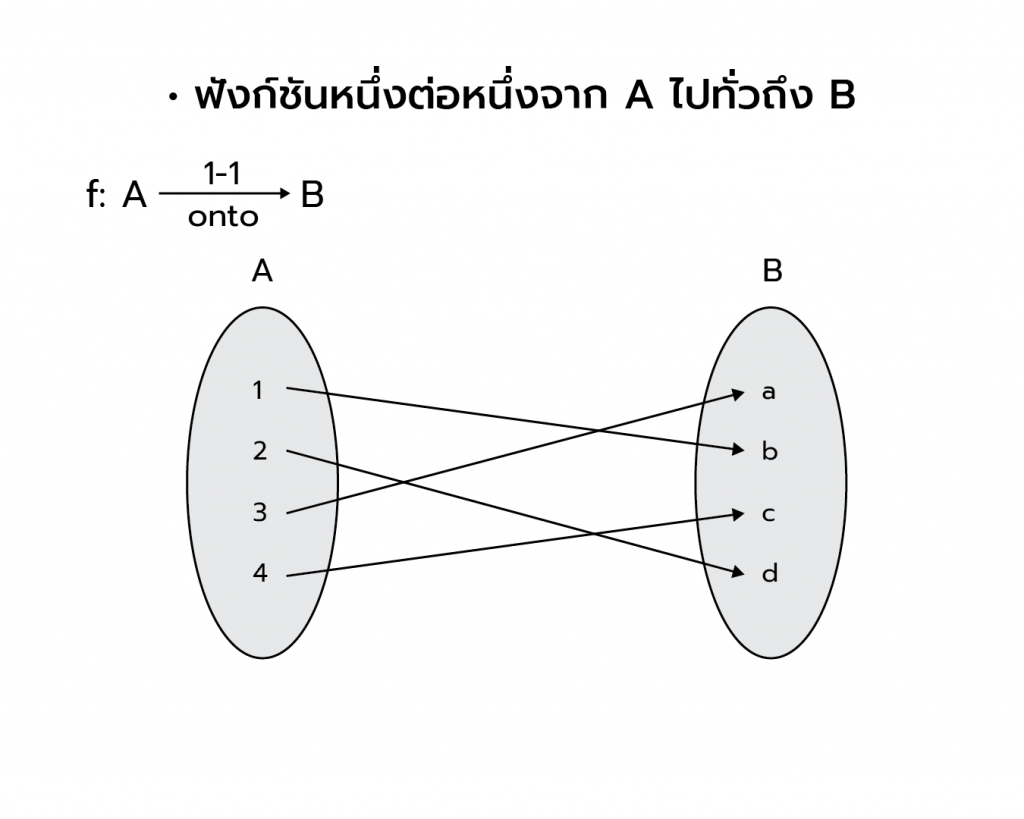
ฟังก์ชันหนึ่งต่อหนึ่งจาก A ไปทั่วถึง B
ถ้า f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไป B และ f เป็นฟังก์ชันจาก A ไปทั่วถึง B แล้ว f เป็นฟังก์ชันหนึ่งต่อหนึ่งจาก A ไปทั่วถึง B เขียนแทนด้วย f:A 1-1 onto→ B
ฟังก์ชันผกผันหรือฟังก์ชันอินเวอร์ส ให้ f เป็นฟังก์ชันใด ๆ อินเวอร์สของฟังก์ชัน f เขียนแทนด้วย f⁻¹
ถ้า f⁻¹ เป็นฟังก์ชัน จะเรียก f⁻¹ นี้ว่า ฟังก์ชันอินเวอร์ส ถ้า f⁻¹ เป็นฟังก์ชันของ x จะเขียนได้ว่า f⁻¹(x)โดยวิธีหา f⁻¹ จะเหมือนกับการหา r⁻¹ (ความสัมพันธ์อินเวอร์ส) เช่น
ฟังก์ชัน y = 3x + 7
อินเวอร์สของฟังก์ชันนี้ คือ x = 3y + 7 (ได้จากการสลับชื่อตัวแปร)
จากนั้น จัดรูปใหม่ให้ y มาอยู่ด้านซ้ายของสมการ จะได้ y = ![]()
จะเขียนได้ว่า f = {(1, 2), (2, 4), (3, 8), (4, 7)}
f⁻¹ = {(2, 1), (4, 2), (8, 3), (7, 4)}
ข้อสังเกต
- f⁻¹ อาจไม่เป็นฟังก์ชัน
- f⁻¹ จะเป็นฟังก์ชัน ก็ต่อเมื่อ f เป็นฟังก์ชันหนึ่งต่อหนึ่ง
- ถ้า f⁻¹ เป็นฟังก์ชัน แล้ว f(a) = b จะได้ว่า f⁻¹(b) = a
การดำเนินการของฟังก์ชันให้ f และ g เป็นฟังก์ชันที่มีโดเมน และเรนจ์เป็นสับเซตของจำนวนจริง จะมีวิธีการดำเนินการระหว่างฟังก์ชันดังนี้ วิธีการดำเนินการระหว่างฟังก์ชัน
ตัวอย่างโจทย์ ให้ (x) = 2x + 3 และ g(x) = x² – 1 จงหา (f – g)(2) เฉลย
คุยกันท้ายบท
จะเห็นได้ว่าความสัมพันธ์ และฟังก์ชัน เป็นพื้นฐานส่วนสำคัญในการต่อยอดไปในบทถัดไปก็คือ “ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม” ซึ่งในบทถัดไปฟังก์ชันเหล่านี้จะมีความซับซ้อนเพิ่มขึ้นไปอีก ในคณิตศาสตร์ ม.4 เทอม 2 จะมีความเชื่อมโยงจากบท “ความสัมพันธ์ และฟังก์ชัน” อยู่ตลอด และควรให้ความสำคัญกับการเรียนเพื่อความเข้าใจสูงสุด ในเนื้อหาบทเรียนต่างๆ ฝึกทำโจทย์บ่อยๆ และใช้เวลาว่างบนหน้าเว็บไซต์ของ Panya Society ฝึกทำโจทย์ที่พี่แทรกไว้ พร้อมคำนวณตามไปด้วย เพื่อให้ได้ประโยชน์จากการทบทวนความรู้…อย่าแอบดูเฉลยนะ!
พี่หวังว่า น้องๆจะสนุกกับการเรียนคณิตศาสตร์ ม.4 เทอม 2 ไปตลอดทั้งเทอม และขอให้น้องๆประสบความสำเร็จในการเรียนเทอมนี้ ได้เกรดดังหวัง คะแนนปังทุกคนเลยครับ
ความสัมพันธ์ และฟังก์ชัน
- อดีต Senior Software Engineer ที่ Google กว่า 10 ปี
- ได้รับทุนเล่าเรียนหลวงไปศึกษาระดับปริญญาตรี ด้าน Electrical and Computer Engineering และ Computer Science ที่ Carnegie Mellon University สหรัฐอเมริกา
- จบปริญญาเอก ด้าน Artificial Intelligence พร้อมรางวัลนักเรียนดีเด่นจาก UCLA
- ผลงานวิจัยด้าน Artificial Intelligence (AI) ของพี่นอตได้รับรางวัลงานวิจัยดีเยี่ยมจาก สำนักงานคณะกรรมการวิจัยแห่งชาติในปี 2557
ทำความรู้จัก พี่นอต (ดร.ธรรมนิติ์ พิพัฒน์ศรีสวัสดิ์)
Math Magic



















