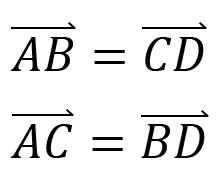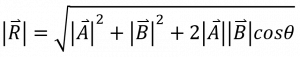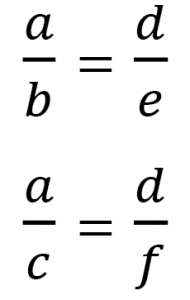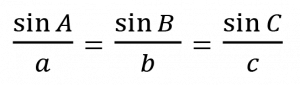PANYA SOCIETY
แรงและกฎการเคลื่อนที่

สรุปเนื้อหาที่สำคัญ
เดินทางมาสู่บทที่ 3 ของฟิสิกส์ ม. 4 เทอม 1 “แรงและกฎการเคลื่อนที่” ซึ่งนับว่าเป็นบทสำคัญอย่างยิ่ง เพราะเป็นพื้นฐานที่สำคัญในการเรียนบทต่อ ๆ ไป ในวิชาฟิสิกส์ ม. ปลาย และในสถิติข้อสอบ TCAS สัดส่วนการออกข้อสอบบทนี้ในปีที่ผ่าน ๆ มา ของข้อสอบ 9 วิชาสามัญ พบความถี่ในการออกข้อสอบโดยเฉลี่ยประมาณ 1 ข้อในทุกปี
นับว่าบทเรียนฟิสิกส์ ม.4 เทอม 1 เรื่อง “แรงและกฎการเคลื่อนที่” มีความสำคัญอย่างยิ่งที่น้อง ๆ จะต้องทำความเข้าใจเนื้อหาโดยละเอียด และอัดพื้นฐานของบทนี้ให้แน่น เพื่อพร้อมรับมือกับการทำข้อสอบที่มีความหลากหลาย และควรฝึกทำโจทย์ที่ประยุกต์หลายบทเข้าไว้ด้วยกัน ที่มีเนื้อหาร่วมกับบทนี้
อย่างที่กล่าวข้างต้น แรงและกฎการเคลื่อนที่ ออกข้อสอบทุกปี ดังนั้น น้อง ๆ ก็ควรใช้เป็นข้อที่ทำคะแนนอย่างยิ่ง เพื่อให้การอ่านหนังสือเตรียมสอบเข้ามหาวิทยาลัยคุ้มค่าที่สุด
แรงและกฎการเคลื่อนที่ มีหน่วยย่อย ดังนี้
- แรงและการแตกแรง
- กฎการเคลื่อนที่ของนิวตัน
- แรงดึงดูดระหว่างมวล
- แรงในแนวตั้งฉาก
- แรงตึงเชือก
- แรงเสียดทาน
แรงและการแตกแรง
แรง
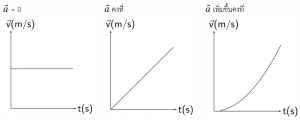
แรงเป็นการกระทำที่ผลักหรือดึง เป็นปริมาณเวกเตอร์
ถ้าแรงลัพธ์ที่กระทำกับวัตถุไม่เท่ากับศูนย์ วัตถุจะเปลี่ยนสภาพการเคลื่อนที่
แรงมี 2 ประเภทใหญ่ ๆ
1. แรงที่ต้องสัมผัส
คือ แรงที่ต้องสัมผัสวัตถุก่อนถึงจะเกิดแรงได้
เช่น การผลักของ การดึงของ การเตะ การต่อย เป็นต้น
2. แรงที่ไม่ต้องสัมผัส
คือ แรงที่ไม่ต้องสัมผัสวัตถุก็เกิดแรงได้
เช่น แรงโน้มถ่วง แรงเเม่เหล็ก เเรงทางไฟฟ้า เป็นต้น
การรวมแรง
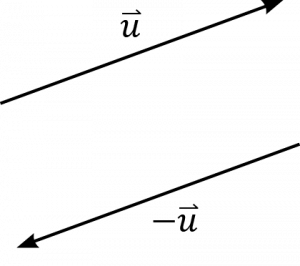
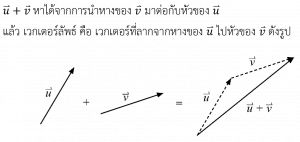
เหมือนการรวมเวกเตอร์ทั่วไป โดยมีวิธีรวมแรงดังนี้
1. วาดรูป
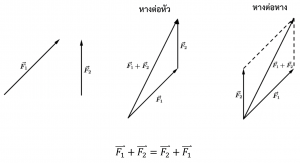
2. การคำนวณ
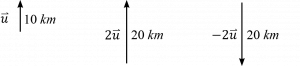
2.1 แรงอยู่บนเส้นตรงเดียวกัน
กำหนดทิศใดทิศหนึ่งเป็นบวก ทิศที่ตรงข้ามกับทิศที่กำหนดจะเป็นลบ แล้วนำขนาดมารวมกันตามเครื่องหมายที่ได้ คำตอบถ้าออกมาเป็นค่าบวกก็มีทิศเดียวกับทิศที่กำหนดให้เป็นบวก ถ้าคำตอบที่ได้มีค่าลบก็มีทิศตรงข้ามกับที่กำหนด
เช่น
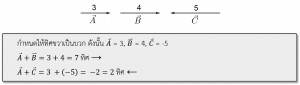
2.2 แรงตั้งฉากกัน
ขนาดของแรงลัพธ์จะหาได้ด้วยวิธีพีทาโกรัส
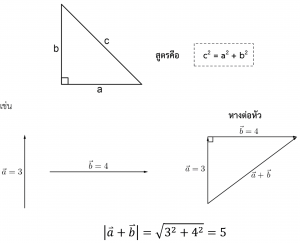
2.3 แตกแรง
จากการที่เราสามารถรวมแรงเป็นแรงลัพธ์ได้ ในบางกรณีก็อาจแตกเเรงออกเพื่อให้สะดวกต่อการใช้งานได้
โดยมีขั้นตอนการแตกแรงดังนี้
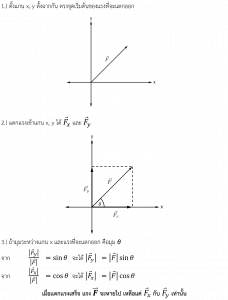
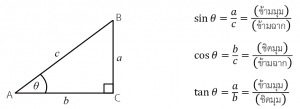
* จะแตกแรงโดยใช้ cos หรือ sin ต้องพิจารณาว่า แรงทำมุมกับแกนใด *
กฎการเคลื่อนที่ของนิวตัน
มีอยู่ทั้งหมด 3 ข้อ
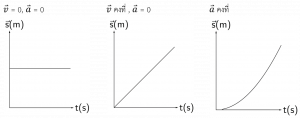
1. วัตถุจะคงสภาพหยุดนิ่ง หรือเคลื่อนที่ด้วยความเร็วคงที่เป็นเส้นตรง เว้นแต่จะถูกกระทำด้วยแรงทำให้เปลี่ยนสภาพการเคลื่อนที่

ใช้เมื่อ v = 0 หรือ v คงที่
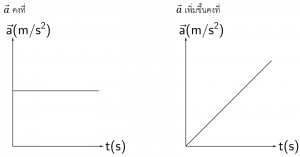
2. ความเร่งของวัตถุแปรผันตรงกับแรงลัพธ์ที่กระทำต่อวัตถุ และแปรผกผันกับมวลของวัตถุ

ใช้เมื่อ แรงลัพธ์ไม่เท่ากับศูนย์ หรือ มีความเร่ง
3. แรงที่วัตถุที่ 1 กระทำต่อวัตถุที่ 2 มีขนาดเท่ากับแรงที่วัตถุที่ 2 กระทำต่อวัตถุที่ 1 แต่มีทิศตรงข้าม

แรงดึงดูดระหว่างมวล
วัตถุที่มีมวลจะมีแรงดึงดูดซึ่งกันและกัน ซึ่งแรงทั้งสองจะมีขนาดเท่ากันแต่มีทิศตรงกันข้าม ดังรูป
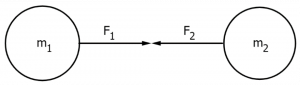
ซึ่ง F1 มีขนาดเท่ากับ F2
ขนาดของแรงทั้งสองสามารถคำนวณได้จากสูตร

โดยที่ FG คือ แรงดึงดูดระหว่างมวล
G คือ ค่าโน้มถ่วงสากล มีค่าเท่ากับ 6.67 × 10-11 นิวตัน·เมตร2/กิโลกรัม2
R คือ ระยะห่างระหว่างมวลทั้งสอง
มวลทุกมวลจะมีแรงดึงดูดระหว่างกัน เช่น มนุษย์ 2 คนก็มีแรงดึงดูดเข้าหากัน แต่แรงนั้นมีค่าน้อยมาก ๆ ทำให้ไม่รู้สึกว่ามีแรงดึงดูดอยู่ แรงนี้จะมีผลกับวัตถุที่มีมวลมาก ๆ เช่น โลก ดาวเคราะห์ต่าง ๆ เป็นต้น
แรงในแนวตั้งฉาก
ถ้าเรามีวัตถุวางอยู่นิ่งบนพื้น จะมีแรงโน้มถ่วงของโลกมากระทำต่อวัตถุนั้น จากกฎข้อที่ 1 ของนิวตัน คือ ΣF = 0 แสดงว่าต้องมีแรงต้านที่ต้านแรงโน้มถ่วงเพื่อทำให้วัตถุอยู่นิ่งได้ นั่นคือแรงที่พื้นดันวัตถุนั่นเอง เราเรียกเเรงนั้นว่า แรงในแนวตั้งฉาก (FN) และค่าของแรงในแนวตั้งฉากเป็นได้หลายค่า
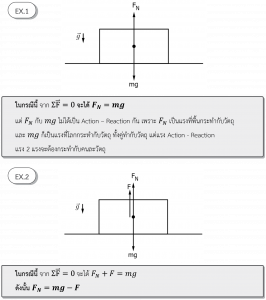
คุณสมบัติของแรงในแนวตั้งฉาก
1. มีทิศตั้งฉากกับพื้นผิวเสมอ
2. มีอยู่เมื่อวัตถุกดลงบนพื้นผิว
แรงตึงเชือก
ถ้าเรามีวัตถุที่ห้อยอยู่นิ่งบนเพดานด้วยเชือกเบาจะมีแรงโน้มถ่วงมากระทำต่อวัตถุนั้น ในกรณีนี้แรงที่มาต้านแรงโน้มถ่วงคือ แรงตึงเชือก (FT)
คุณสมบัติของแรงตึงเชือก
1. ถ้าเชือกไม่มีมวล การดึงเชือกที่ไม่มีมวลที่ผูกติดกับวัตถุจะเหมือนกับการดึงวัตถุธรรมดา
2. ขนาดของเเรงตึงเชือกจะมีค่าเท่ากันทั้งเส้น
3. ทิศทางของแรงตึงเชือกขนานกับเชือกทุก ๆ จุดบนเส้นเชือก ทำให้สามารถใช้เชือกเป็นอุปกรณ์ในการเปลี่ยนทิศทางของแรงได้
การวัดค่าแรงตึงเชือกเราสามารถเอาตาชั่งสปริงมาชั่งระหว่างกลางเส้นเชือกตรงจุดที่เราอยากหาแรงตึงเชือก โดยค่าที่อ่านได้จากตาชั่งสปริงจะเป็นค่าของแรงตึงเชือกนั่นเอง
แรงเสียดทาน
คือ เเรงที่ต้านการเคลื่อนที่ ซึ่งเกิดขึ้นระหว่างผิวสัมผัสของวัตถุ ตัวย่อคือ f
แรงเสียดทานมี 2 ชนิด
1. แรงเสียดทานสถิต (fs)
คือ แรงเสียดทานที่เกิดขึ้นระหว่างพื้นผิวกับวัตถุ โดยที่มีแรงมากระทำกับวัตถุในแนวขนานกับพื้นผิว แต่วัตถุไม่เคลื่อนที่ ค่าของแรงเสียดทานสถิตจะมีได้หลายค่า โดยมีค่าเท่ากับแรงที่มากระทำกับวัตถุแต่วัตถุไม่เคลื่อนที่ จนมีค่ามากสุดคือ แรงเสียดทานสถิตมากสุด (fsmax)

โดย μs คือ สัมประสิทธิ์ความเสียดทานสถิต
2. แรงเสียดทานจลน์ (fk)
คือ แรงเสียดทานที่เกิดระหว่างพื้นผิวกับวัตถุขณะที่วัตถุเคลื่อนที่ แรงเสียดทานจลน์จะคงที่ตลอด และจะมีค่าน้อยกว่าค่าเเรงเสียดทานสถิตมากสุด ในพื้นผิวสัมผัสเดียวกัน

โดย μk คือ สัมประสิทธิ์ความเสียดทานจลน์
***ค่า μs จะมีค่ามากกว่า μk เสมอบนพื้นผิวเดียวกัน***
คุณสมบัติของแรงเสียดทาน
- มีทิศขนานกับพื้นผิว
- มีทิศต้านการเคลื่อนที่ของวัตถุ ไม่มีทางที่จะส่งเสริมการเคลื่อนที่ให้เร็วขึ้น
- วัตถุจะต้องสัมผัสพื้นผิวถึงจะมีแรงเสียดทาน
คุยกันท้ายบท
จะเห็นได้ว่า “แรงและกฎการเคลื่อนที่” ในฟิสิกส์ ม.4 เทอม 1 เป็นพื้นฐานในการเรียนวิชาฟิสิกส์ ซึ่งถ้าน้องคนไหน ไม่มีความรู้ความเข้าใจที่แท้จริงก็จะยิ่งสร้างปมปัญหาต่อมาถึงบทถัดไป ดังนั้น ควรทบทวน “แรงและกฎการเคลื่อนที่” ให้คล่องที่สุด
ที่สำคัญคือ อย่าลืมฝึกทำโจทย์บ่อย ๆ และใช้เวลาว่างบนหน้าเว็บไซต์ของ Panya Society ลองฝึกทำโจทย์ที่พี่ให้ไว้ หรือเข้าไปชมตัวอย่างวิดีโอการสอนต่าง ๆ พร้อมคิดคำนวณตามไปด้วย เพื่อให้ได้ประโยชน์จากการทบทวนความรู้ครับ แล้วพบกันในเทอมต่อไป เข้มข้นยิ่งขึ้นกับ “ฟิสิกส์ ม.4 เทอม 2” มีรูปแบบการคิดแบบใหม่ สนุกแน่นอนครับผม 🙂
พี่หวังว่า น้อง ๆ จะสนุกกับการเรียนฟิสิกส์ ม.4 เทอม 1 ไปตลอดทั้งเทอม ขอให้น้อง ๆ ประสบความสำเร็จในการเรียน ได้เกรดดังหวัง คะแนนปังทุกคนเลยครับ แวะไปชมเนื้อหาบทต่อไปของฟิสิกส์ ม.4 เทอม 1 กันด้วยนะ…อย่าเทพี่แชร์กลางทางนะครับ
- ปัจจุบันทำงานในบริษัท Start-up ด้านเทคโนโลยีหลายแห่ง
- อดีตเหรียญทองฟิสิกส์โอลิมปิก
- เคยทำงานที่บริษัท Oracle สหรัฐอเมริกา ซึ่งเป็นบริษัทซอฟต์แวร์ระดับ Top 5 ของโลก
- ผู้ร่วมก่อตั้งเว็บไซต์เด็กดีดอทคอม