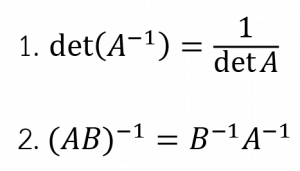PANYA SOCIETY
เวกเตอร์
สรุปเนื้อหาที่สำคัญ
เดินทางมาสู่บทที่ 3 ของคณิตศาสตร์ ม. 5 เทอม 1 “เวกเตอร์” ก็นับว่าเป็นบทสำคัญอย่างยิ่งอีกเช่นกัน เพราะในสถิติข้อสอบ TCAS สัดส่วนการออกข้อสอบบทนี้ ในปีที่ผ่าน ๆ มา ในข้อสอบ A – Level พบความถี่ในการออกข้อสอบโดยเฉลี่ยถึงประมาณ 2 ข้อในทุกปี
นับว่าบทเรียนคณิตศาสตร์ ม. 5 เทอม 1 เรื่อง “เวกเตอร์” มีความสำคัญอย่างยิ่งที่น้อง ๆ จะต้องทำความเข้าใจเนื้อหาโดยละเอียด และอัดพื้นฐานของบทนี้ให้แน่น เพื่อพร้อมรับมือกับการทำข้อสอบที่มีความหลากหลาย และควรฝึกทำโจทย์ที่ประยุกต์หลายบทเข้าไว้ด้วยกัน ที่มีเนื้อหาร่วมกับบทนี้
อย่างที่กล่าวข้างต้น เวกเตอร์ มีออกข้อสอบทุกปี ดังนั้น น้อง ๆ ก็ควรใช้เป็นข้อที่ทำคะแนนอย่างยิ่ง เพื่อให้การอ่านหนังสือเตรียมสอบเข้ามหาวิทยาลัยคุ้มค่าที่สุด
เวกเตอร์ มีหน่วยย่อย ดังนี้
- เวกเตอร์และสมบัติของเวกเตอร์
- เวกเตอร์ในระบบพิกัดฉาก
- ผลคูณเชิงสเกลาร์
- ผลคูณเชิงเวกเตอร์
เวกเตอร์และสมบัติของเวกเตอร์
เวกเตอร์
เป็นปริมาณที่มีทั้งขนาดและทิศทาง
เช่น การบอกทางให้คนเดินไป ถ้าบอกแค่ว่า เดินไป 10 ก้าว จะยังไม่รู้ว่าต้องเดินไปทางไหน ต้องบอกว่า เดินไปในทิศทางไหนด้วย
เนื่องจากเวกเตอร์เป็นปริมาณที่บอกขนาดและทิศทางเท่านั้น ไม่ได้จำกัดว่าจะต้องเริ่มจากจุดใดและไปจบที่จุดใด
ดังนั้นเราสามารถเลื่อนเวกเตอร์ได้ แต่ต้องไม่เปลี่ยนขนาดและทิศทางของเวกเตอร์นั้น
เช่น พิจารณาสี่เหลี่ยมด้านขนาน
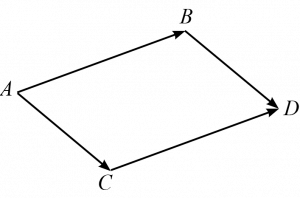
จะได้ว่า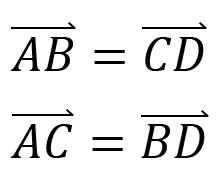
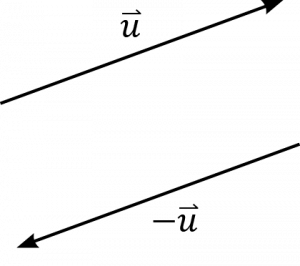
เมื่อมีเวกเตอร์หนึ่งที่มีขนาดเท่ากับเวกเตอร์ u แต่มีทิศตรงข้ามกัน จะเรียกเวกเตอร์นั้นว่า -u
การบวกเวกเตอร์
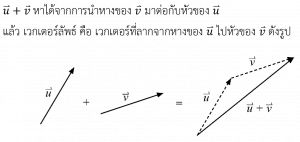
* การลบเวกเตอร์ u – v จะหาได้จาก v + (-u)
การคูณด้วยสเกลาร์
การคูณค่าคงที่ c กับเวกเตอร์หนึ่ง จะทำให้ขนาดของเวกเตอร์นั้นเพิ่มขึ้นเป็น c เท่า
– ถ้า c เป็นบวก เวกเตอร์ที่ได้จะมีทิศทางเดิม
– ถ้า c เป็นลบ เวกเตอร์ที่ได้จะมีทิศทางตรงกันข้าม
เช่น
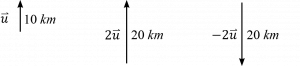
สมบัติการบวกเวกเตอร์และการคูณเวกเตอร์ด้วยสเกลาร์

เวกเตอร์ในระบบพิกัดฉาก
ให้ u เป็นเวกเตอร์ที่ลากจากจุด x1, y1, z1 ไปยัง x2, y2, z2 ในระบบพิกัดฉากสามมิติ ดังรูป
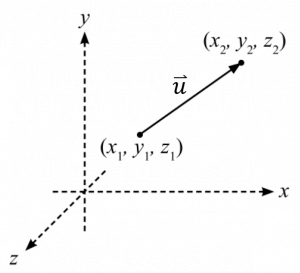
จะสามารถเขียนเวกเตอร์ในรูปคู่อันดับ ได้ดังนี้
(x2 – x1, y2 – y1, z2 – z1)
หรือสามารถเขียนในรูปเมทริกซ์หลัก ได้ดังนี้
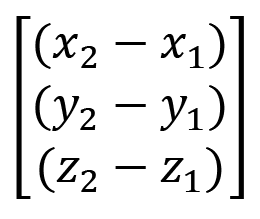
ขนาดของเวกเตอร์
ขนาดของเวกเตอร์ ก็คือ ความยาวของเวกเตอร์นั้น โดยไม่คำนึงถึงทิศทาง
ขนาดของเวกเตอร์ u เขียนแทนด้วย |u|
เมื่อเวกเตอร์ u = (a, b, c) จะสามารถหาขนาดของเวกเตอร์ ได้จาก
![]()
เวกเตอร์หนึ่งหน่วย
จะหาเวกเตอร์หนึ่งหน่วย ที่มีทิศทางเดียวกับเวกเตอร์ u ได้จาก
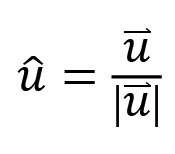
ผลคูณเชิงสเกลาร์

สมบัติของผลคูณเชิงสเกลาร์

ผลคูณเชิงเวกเตอร์

สมบัติของผลคูณเชิงเวกเตอร์

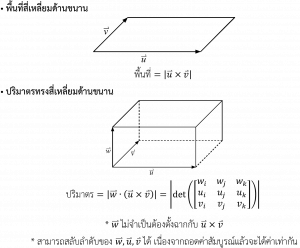
การประยุกต์ใช้ผลคูณเชิงเวกเตอร์
คุยกันท้ายบท
จะเห็นได้ว่า “เวกเตอร์” ในคณิตศาสตร์ ม. 5 เทอม 1 จะมีความเชื่อมโยงกับบทที่ผ่านมาคือ “เมทริกซ์” ซึ่งถ้าน้องคนไหน ไม่มีความรู้ความเข้าใจที่แท้จริงจากบทก่อนหน้านี้ ก็จะยิ่งสร้างปมปัญหาต่อมาถึงบทนี้ ดังนั้น ควรกลับไปทบทวน “เมทริกซ์” จะได้นำความรู้ความเข้าใจจากบทที่แล้ว มาต่อยอดได้ในเนื้อหาของบทนี้
ที่สำคัญคือ อย่าลืมฝึกทำโจทย์บ่อย ๆ และใช้เวลาว่างบนหน้าเว็บไซต์ของ Panya Society ลองฝึกทำโจทย์ที่พี่ให้ไว้ หรือเข้าไปชมตัวอย่างวิดีโอการสอนต่าง ๆ พร้อมคิดคำนวณตามไปด้วย เพื่อให้ได้ประโยชน์จากการทบทวนความรู้ครับ แล้วพบกันในเทอมต่อไป เข้มข้นยิ่งขึ้นกับ “ม.5 เทอม 2” มีรูปแบบการคิดแบบใหม่ สนุกแน่นอนครับผม 🙂
พี่หวังว่า น้อง ๆ จะสนุกกับการเรียนคณิตศาสตร์ ม.5 เทอม 1 ไปตลอดทั้งเทอม ขอให้น้อง ๆ ประสบความสำเร็จในการเรียน ได้เกรดดังหวัง คะแนนปังทุกคนเลยครับ แวะไปชมเนื้อหาบทต่อไปของคณิตศาสตร์ ม.5 เทอม 2 กันด้วยนะ…อย่าเทพี่นอตกลางทางนะครับ
- อดีต Senior Software Engineer ที่ Google กว่า 10 ปี
- ได้รับทุนเล่าเรียนหลวงไปศึกษาระดับปริญญาตรี ด้าน Electrical and Computer Engineering และ Computer Science ที่ Carnegie Mellon University สหรัฐอเมริกา
- จบปริญญาเอก ด้าน Artificial Intelligence พร้อมรางวัลนักเรียนดีเด่นจาก UCLA
- ผลงานวิจัยด้าน Artificial Intelligence (AI) ของพี่นอตได้รับรางวัลงานวิจัยดีเยี่ยมจาก สำนักงานคณะกรรมการวิจัยแห่งชาติในปี 2557
ตัวอย่างการสอน โดยพี่นอต
Math Magic