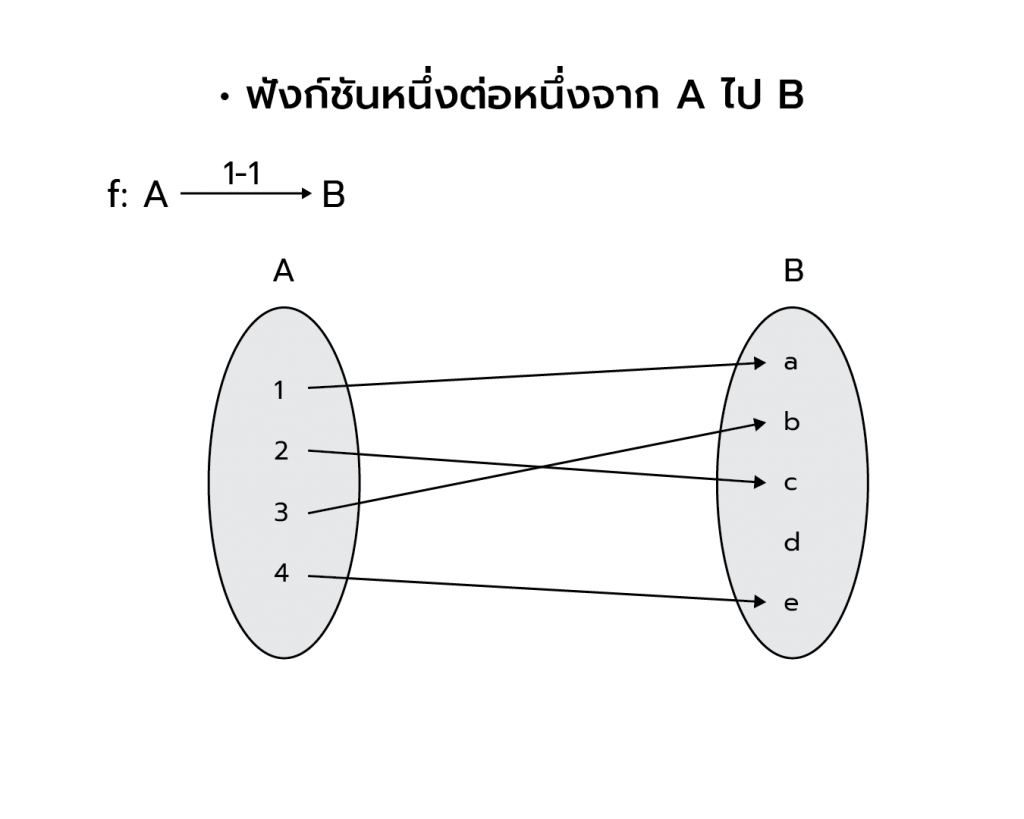
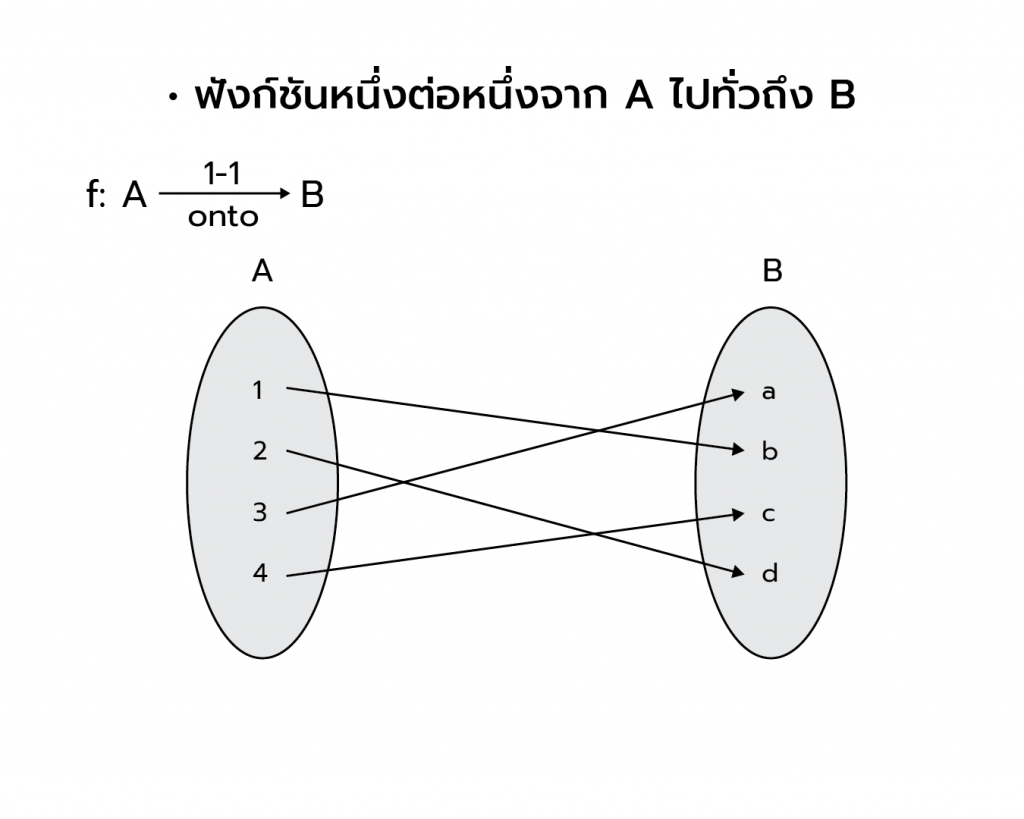
สรุปเนื้อหาที่สำคัญ
เดินทางมาสู่บทที่ 2 ของคณิตศาสตร์ ม. 4 เทอม 2 “ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม” ก็นับว่าเป็นบทสำคัญอย่างยิ่งอีกเช่นกัน เพราะในสถิติข้อสอบ TCAS สัดส่วนการออกข้อสอบบทนี้ ในปีที่ผ่านๆมา ในข้อสอบ A – Level พบความถี่ในการออกข้อสอบสูงสุด โดยเฉลี่ยถึงประมาณ 3-4 ข้อในทุกปี
นับว่าบทเรียนคณิตศาสตร์ ม.4 เทอม 2 เรื่อง “ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม” มีความสำคัญอย่างยิ่งที่น้องๆจะต้องทำความเข้าใจเนื้อหาโดยละเอียด และอัดพื้นฐานของบทนี้ให้แน่น เพื่อพร้อมรับมือกับการทำข้อสอบที่มีความหลากหลาย และควรฝึกทำโจทย์ที่ประยุกต์หลายบทเข้าไว้ด้วยกัน ที่มีเนื้อหาร่วมกับบทนี้
อย่างที่กล่าวข้างต้น ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม ออกข้อสอบหลายข้อจริงๆ ดังนั้น น้องๆก็ควรใช้เป็นข้อที่ทำคะแนนอย่างยิ่ง เพื่อให้การอ่านหนังสือเตรียมสอบเข้ามหาวิทยาลัยคุ้มค่าที่สุด อ่าน 1 บทก็ควรเก็บคะแนนได้ทุกประเภทข้อสอบ นำไปใช้ประยุกต์ได้กับข้อสอบเข้ามหาวิทยาลัย TCAS ในข้อสอบ A – Level ห้ามทิ้ง!
ชันฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม มีหน่วยย่อย ดังนี้
- เลขยกกำลัง
- การเปรียบเทียบเลขยกกำลัง
- สมการรากที่สอง
- รูปแบบรูทไม่รู้จบ
- ฟังก์ชันเอกซ์โพเนนเชียล
- กราฟของฟังก์ชันเอกซ์โพเนนเชียล และการแปลงกราฟ
- สมการเอกซ์โพเนนเชียล
- อสมการเอกซ์โพเนนเชียล
- ฟังก์ชันลอการิทึม
- กราฟของฟังก์ชันลอการิทึม และการแปลงกราฟ
- สมบัติของฟังก์ชันลอการิทึม
- การเปรียบเทียบค่าลอการิทึม
- แมนทิสซา และคาแรกเทอริสติก
- สมการลอการิทึม
- อสมการลอการิทึม
เลขยกกำลัง
สมบัติของเลขยกกำลัง ให้ a,b,m และ n เป็นค่าคงที่ใดๆ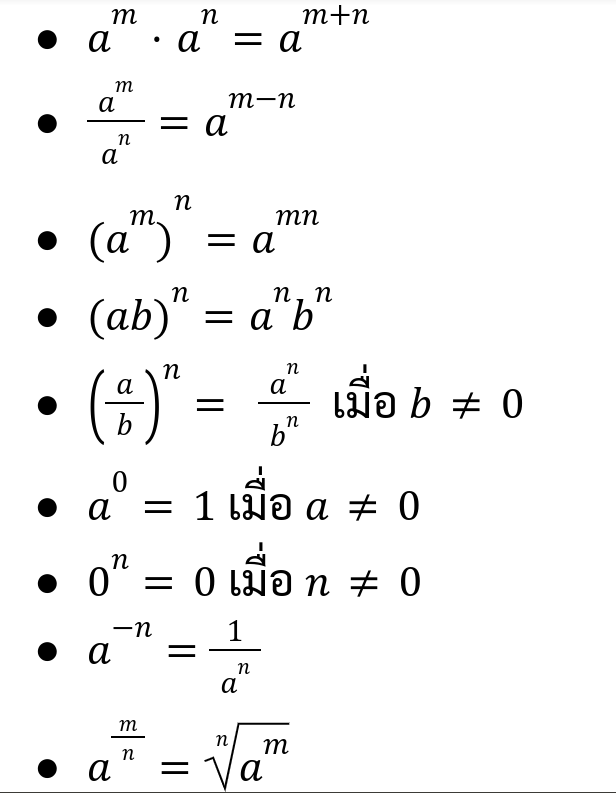
ตัวอย่างโจทย์ จงใช้สมบัติของเลขยกกำลังทำให้อยู่ในรูปแบบง่าย ((73)-2)0.5 เฉลย
การเปรียบเทียบเลขยกกำลัง
- ถ้า เลขฐาน > 1 แล้ว เลขชี้กำลังมากค่าจะยิ่งมาก
- ถ้า 0 < เลขฐาน < 1 แล้ว เลขชี้กำลังมากค่าจะยิ่งน้อย
การเปรียบเทียบเลขยกกำลัง มีวิธีการได้แก่
ทำฐานให้เท่ากัน โดยพยายามจัดรูปให้เลขฐานเท่ากัน โดยหาเลขฐานร่วม แล้วแปลงเลขฐานเดิมของเลขที่จะเปรียบเทียบกันให้อยู่ในรูปยกกำลังของเลขฐานร่วม ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม เช่น
44 เปรียบเทียบกับ 83
(22)4 =28 เปรียบเทียบกับ (23)3=29
จะได้ว่า 28 < 29 เพราะฉะนั้น 44 <83
ทำเลขชี้กำลังให้เท่ากัน ถ้าเลขฐานเท่ากัน เลขฐานมากค่าจะยิ่งมาก เลขฐานน้อยค่าจะยิ่งน้อย ดังนั้น ถ้าจัดรูปให้เลขชี้กำลังเท่ากันได้ ก็จะสามารถเปรียบเทียบเลขฐานได้เลย เช่น
166 เปรียบเทียบกับ 274
(42)6 = 412 เปรียบเทียบกับ (33)4 = 312
จะได้ว่า 412 > 312 เพราะฉะนั้น 166 > 274
กรณีเลขฐานติดลบ ให้พิจารณาว่า ถ้ายกกำลังแล้วยังติดลบอยู่หรือไม่ โดยแปลงเลขฐานเป็น -1 คูณกับ จำนวนที่เป็นบวก แล้วกระจายเลขยกกำลังเข้าไป แล้วพิจารณาว่าหลังกระจายเลขยกกำลังเข้าไปแล้ว -1 ยังคงอยู่หรือไม่
โดยพิจารณาดังนี้
- ถ้า -1 ยกกำลังด้วยเลขคู่ จะได้ 1
- ถ้า -1 ยกกำลังด้วยเลขคี่ จะได้ -1
- ถ้า -1 ยกกำลังด้วยเศษส่วนโดยที่ตัวส่วนเป็นเลขคี่ แล้ว
- ถ้าเศษเป็นเลขคู่ จะได้ 1
- ถ้าเศษเป็นเลขคี่ จะได้ -1
- ถ้า -1 ยกกำลังด้วยเศษส่วนโดยที่ตัวส่วนเป็นเลขคู่ จะหาค่าไม่ได้
จากนั้นจึงทำการเปรียบเทียบ โดยถ้ายังติดลบทั้งคู่ ตัวที่ติดลบเยอะกว่า จะมีค่าน้อยกว่า เช่น
(-9)5 เปรียบเทียบกับ (-9)4
(-1 × 9)5 เปรียบเทียบกับ (-1 × 9)4
(-1)5 × 95 เปรียบเทียบกับ (-1)4 × 94
-1 × 95 เปรียบเทียบกับ 1 × 94
จะได้ว่า -95 < 94 เพราะฉะนั้น (-9)5 < (-9)4
ฟังก์ชันเอกโพเนนเชียล
ฟังก์ชันเอกซ์โพเนนเชียล ฟังก์ชันเอกซ์โพเนนเชียลเป็นฟังก์ชันที่ค่าของฟังก์ชันเพิ่มขึ้นหรือลดลงได้เร็วกว่าฟังก์ชันพหุนาม โดยเขียนอยู่ในรูปทั่วไปคร่าว ๆ ได้ว่า
y=ax
โดยที่ a > 0 และ a ≠ 1
ฟังก์ชันเอกโพเนนเชียล สามารถใช้อธิบายสิ่งต่าง ๆ ได้มากมาย เช่น
- การแพร่พันธุ์ของสิ่งมีชีวิต
- การคิดดอกเบี้ยทบต้น
- การเติบโตของเครือข่ายโซเชียล (Social Network)
- การสลายตัวของธาตุกัมมันตรังสี
- การเย็นตัวของวัตถุร้อน
สมบัติของฟังก์ชันเอกซ์โพแนนเชียล
- เมื่อ a > 1 ฟังก์ชัน y = ax จะเป็นฟังก์ชันเพิ่ม
- เมื่อ 0 < a < 1 ฟังก์ชัน y = ax จะเป็นฟังก์ชันลด
- โดเมนของฟังก์ชัน คือ R
- เรนจ์ของฟังก์ชัน คือ R+
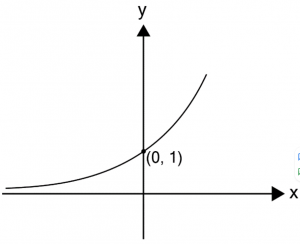
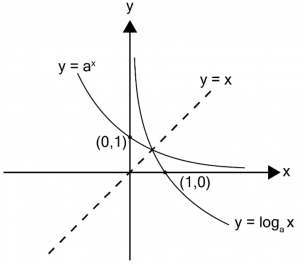
กราฟของฟังก์ชันเอกซ์โพเนนเชียล หากวาดกราฟของฟังก์ชันเอกซ์โพเนนเชียล y = ax จะได้ดังนี้
เมื่อ a > 1
ข้อสังเกต
- กราฟของฟังก์ชันผ่านจุด (0, 1) เสมอ
- กราฟของฟังก์ชันอยู่เหนือแกน x เสมอ
- กราฟของฟังก์ชัน y = ax และ y = (1/a)x = a-x จะสมมาตรกัน โดยมีแกน y เป็นแกนสมมาตร
การแปลงกราฟเอกซ์โพเนนเชียล กราฟของสมการจะเหมือนกับกราฟเอกซ์โพเนนเชียล y = ax ไปทางขวา h หน่วย และเลื่อนขึ้นไป k หน่วย ดังนั้น เพื่อที่จะวาดกราฟเอกซ์โพเนนเชียลให้ได้ง่ายขึ้น อาจจัดรูปสมการให้อยู่ในรูป y-k = ax-h ก่อนดังรูป
เมื่อ a > 1
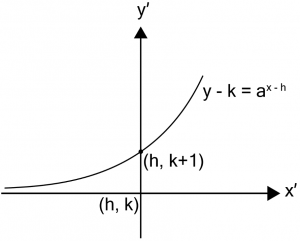
ตัวอย่างโจทย์ จงวาดกราฟคร่าว ๆ ของสมการต่อไปนี้ y = 32x เฉลย
สมการเอกซ์โพเนนเชียล คือ สมการที่มี x อยู่ในเลขชี้กำลัง
การแก้สมการเอกซ์โพเนนเชียล
- แก้โดยการทำฐานให้เท่ากัน
- จัดรูปให้ทั้งสองข้างของสมการมีเลขฐานเท่ากัน
- จะได้ว่า เลขชี้กำลังของทั้งสองข้าง จะเท่ากัน
- แก้โดยการแทนค่าด้วยตัวแปรอื่น
- หากไม่สามารถจัดรูปให้เลขฐานเท่ากันได้ อาจกำหนดให้พจน์ที่มี x อยู่ในเลขชี้กำลัง เป็นตัวแปรอื่น แล้วจึงค่อยแก้สมการ
ตัวอย่างโจทย์ จงแก้สมการเอกซ์โพเนนเชียลต่อไปนี้
ฟังก์ชันลอการิทึม
ฟังก์ชันลอการิทึม เป็นอินเวอร์สของฟังก์ชันเอกซ์โพเนนเชียล
ดังนั้น ถ้าฟังก์ชันเอกซ์โพเนนเชียลมีสมการเป็น
y = ax , a > 0 , a ≠ 1
แล้วฟังก์ชันลอการิทึมจะมีสมการเป็น
x = ay , a > 0 , a ≠ 1
ซึ่งหากจะเขียนให้อยู่ในรูป y ในเทอมของ x จะเขียนได้เป็น
y = logax
ซึ่งหมายถึง x = ay ดังนั้น ฟังก์ชันลอการิทึม คือ
f = {(x, y) | y = loga x, a > 0, a ≠ 1}
ตัวอย่างเช่น
หาค่าของ log2(32)
ให้ y = log2(32)
จะได้ 2y = 32
2y = 25
จะได้ว่า y = 5
ดังนั้น log2(32) = 5
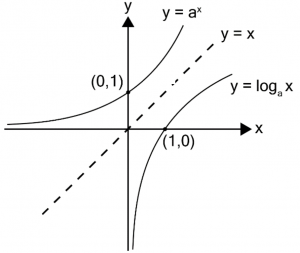
กราฟของฟังก์ชันลอการิทึม เนื่องจากเป็นอินเวอร์สกัน กราฟของฟังก์ชันเอกซ์โพเนนเชียล และกราฟของฟังก์ชันลอการิทึม จึงสมมาตรกันโดยมีเส้นตรง y = x เป็นแกนสมมาตร ดังนี้
กราฟของฟังก์ชันลอการิทึม เมื่อ a > 1
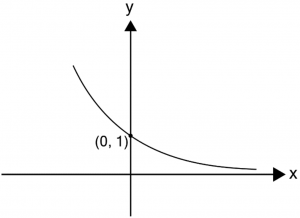
กราฟของฟังก์ชันลอการิทึม เมื่อ 0 < a < 1
สมบัติของลอการิทึม ให้ a, M, N เป็นจำนวนบวก ซึ่ง a > 0 และ a ≠ 1 และ m, n เป็นจำนวนจริงใดๆ
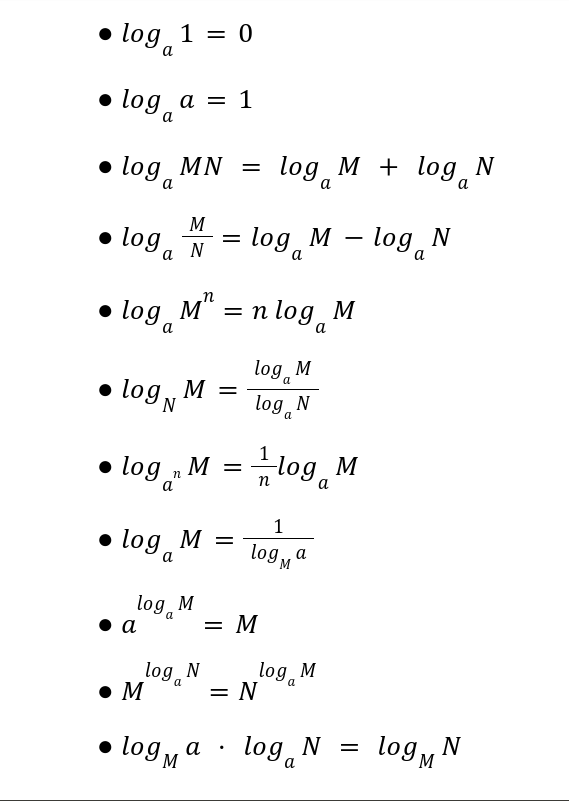
แมนทิสซา และคาแรกเทอริสติก ให้ N เป็นจำนวนจริงบวกใด ๆ และ n เป็นจำนวนเต็ม จะเขียน N ได้ในรูป
N = A×10n โดยที่ 1 ≤ A < 10 จะได้ว่า
- logN = log (A×10n) โดยที่ log1 ≤ logA < log10
- logN = logA + log10n
- logN = logA + nlog10 โดยที่ 0 ≤ logA < 1
- logN = logA + n
เรียก log A ว่า แมสทิสซา ของ log N ซึ่งค่าของ log A จะสามารถหาได้จากการเปิดตารางลอการิทึม
เรียก n ว่า คาแรกเทอริสติก ของ log N
สมการลอการิทึม คือ สมการที่มี x อยู่ในลอการิทึม โดยอาจอยู่ตรงเลขฐาน หรืออยู่หลัง log ก็ได้
การแก้สมการลอการิทึม
- แก้โดยใช้นิยามของฟังก์ชันลอการิทึม
- ถ้า logax = M
- จะได้ว่า x = aM
- แก้โดยการทำฐานให้เท่ากัน
- ถ้า logaM = logaN
- จะได้ว่า M = N
- แก้โดยการแทนค่าด้วยตัวแปรอื่น
- หากจัดรูปสมการไม่ได้อาจแทนค่าตัวที่ติด log ด้วยตัวแปรอื่น แล้วจึงแก้สมการ
ตัวอย่างโจทย์ จงแก้สมการลอการิทึมต่อไปนี้
คุยกันท้ายบท
จะเห็นได้ว่า “ฟังก์ชันเอกซ์โพเนนเชียลและลอการิทึม” ในคณิตศาสตร์ ม.4 เทอม 2 จะมีความเชื่อมโยงกับบทที่ผ่านมาคือ “ความสัมพันธ์ และฟังก์ชัน” ซึ่งถ้าน้องคนไหน ไม่มีความรู้ความเข้าใจที่แท้จริงจากบทที่แล้ว ก็จะยิ่งสร้างปมปัญหาต่อมาถึงบทนี้ ดังนั้น ควรกลับไปทบทวนเพื่อให้ “ความสัมพันธ์ และฟังก์ชัน” จะได้นำความรู้ความเข้าใจจากบทที่แล้ว มาต่อยอดได้ในเนื้อหาของบทที่ 2
ที่สำคัญคือ อย่าลืมฝึกทำโจทย์บ่อยๆ และใช้เวลาว่างบนหน้าเว็บไซต์ของ Panya Society ลองฝึกทำโจทย์ที่พี่ให้ไว้ หรือเข้าไปชมตัวอย่างวิดีโอการสอนต่างๆ พร้อมคิดคำนวณตามไปด้วย เพื่อให้ได้ประโยชน์จากการทบทวนความรู้ครับ แล้วพบกันในบทต่อไป เข้มข้นยิ่งขึ้นกับ “เรขาคณิตวิเคราะห์ และภาคตัดกรวย” กราฟเพียบ กราฟแน่น สนุกแน่นอนครับผม 🙂
พี่หวังว่า น้องๆจะสนุกกับการเรียนคณิตศาสตร์ ม.4 เทอม 2 ไปตลอดทั้งเทอม ขอให้น้องๆประสบความสำเร็จในการเรียน ได้เกรดดังหวัง คะแนนปังทุกคนเลยครับ แวะไปชมเนื้อหาบทสุดท้ายของคณิตศาสตร์ ม.4 เทอม 2 กันด้วยนะ…อย่าเทพี่นอตกลางทางนะครับ
แบบฝึกหัดฟังก์ชันเอ็กซ์โพเนนเชียลและลอการิทึม
- อดีต Senior Software Engineer ที่ Google กว่า 10 ปี
- ได้รับทุนเล่าเรียนหลวงไปศึกษาระดับปริญญาตรี ด้าน Electrical and Computer Engineering และ Computer Science ที่ Carnegie Mellon University สหรัฐอเมริกา
- จบปริญญาเอก ด้าน Artificial Intelligence พร้อมรางวัลนักเรียนดีเด่นจาก UCLA
- ผลงานวิจัยด้าน Artificial Intelligence (AI) ของพี่นอตได้รับรางวัลงานวิจัยดีเยี่ยมจาก สำนักงานคณะกรรมการวิจัยแห่งชาติในปี 2557
ทำความรู้จัก พี่นอต (ดร.ธรรมนิติ์ พิพัฒน์ศรีสวัสดิ์)































































































































 คอร์สเรียน A-Level
คอร์สเรียน A-Level